а) О-центр окружности
АОВ- прямоугольный равнобедренный треуг.
угол О=90 центральный
углы А=В=45
ОА=ОВ=4 катеты
АВ-гипотенуза=4√2
расстояние от центра окр-ти до этой хорды ОВ*sin45=4*√2/2=2√2
б) угол С=45 лежит по другую сторону от центра О от хорды АВ-он вписаный угол , опирается на ту же хорду , что и центральный угол АОВ
--равен половине АОВ/2=90/2=45
теперь дуги дуга АС : дуга СВ = 5 : 4
--на хорде АВ--маленькая дуга АВ и большая АВ(проходит через т.С)
маленькую отсекает угол АСВ=45 град, а большую 315 (360-45)
большую дугуразобьем на 9 частей (5+4) ,
тогда АС =315 * 5/9 = 175 (уголАВС) и СВ =315 * 4/9 = 140(уголВАС)
в) по теореме синусов АВ/sin(ACB)=BC/sin(BAC) ; 4√2/sin45=BC/sin140
BC=4√2/sin45 *sin140=4*sin140
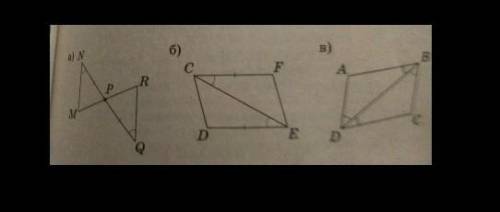
Проведём 2 перпендикулярные прямые (см. рис. 1). Для этого:
1. Из точки на произвольной прямой, проведём окружность произвольного радиуса k.
2. В точках пересечения окружности с прямой, проведём окружности с радиусом p, при это p > k.
3. Через точки пересечений окружностей проводим прямую, она будет перпендикулярна первой прямой.
С циркуля замерим на линейке 6 см и отложим 6 см на одной стороне прямого угла (см. рис. 2).
С транспортира отложим угол в 45° и соединим точки, как показано на рис. 3. Получили искомый треугольник.
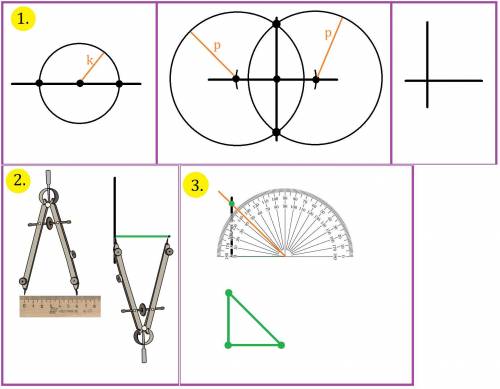
ответ: угол MPN равен с углом QPR так как они вертикальные. Мы знаем что угол N и угол Q равны. Также сторона PQ= NP. Треугольник равны по стороне и двум углам,которые прилежат к ней.
2.угол ECF= Углу DEC как накрест лежащие. Сторона СЕ общая. Треугольники СDE=СFE по двум сторонам и углу между ними.
3.сторона DB общая. Треугольники равны по стороне и двум прилежащим к ней углам
Объяснение: