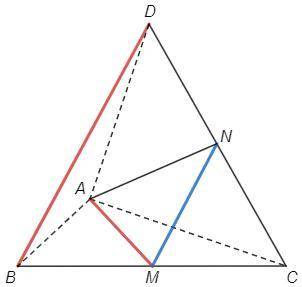
В правильном тетраэдре ABCD точка M - середина BС. Найдите угол между прямыми AM и BD.
Прямая BD пересекает плоскость (ABC) в точке, не лежащей на прямой AM - прямые AM и BD скрещиваются.
Угол между скрещивающимися прямыми - угол между параллельными им пересекающимися прямыми.
Проведем MN||BD
∠AMN - искомый угол.
Правильный тетраэдр, все грани - правильные треугольники.
Пусть все ребра равны а
N - середина CD (т Фалеса)
MN=a/2 (средняя линия)
AM=AN =a√3/2 (медианы в равностороннем треугольнике)
△MAN - равнобедренный
cos(AMN) =MN/2AM =2a/4a√3 =√3/6
∠AMN =arccos(√3/6)
заебено украл ответ
Объяснение:
Параллелограмм ABCD, угол A острый. Высота BE, опущенная на AD, равна 3, высота BF, опущенная на CD, равна 4. По теореме об углах с соответственно перпендикулярными сторонами острый угол параллелограмма равен 45°. Из треугольника ABE⇒AB=3√2; из треугольника CBF⇒BC=AD=4√2⇒S=AB·AD·sin 45°=3√2·4√2·√2/2=12√2