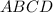 прямоугольная, то значит одна из её сторон перпендикулярна основаниям, а другая – наклонная. При этом есть две диагонали: одна идёт из прямого угла в тупой к короткому основанию, а другая – из прямого в острый к длинному основанию. Та диагональ, которая идёт к длинному основанию лежит напротив тупого угла трапеции, а значит она длиннее и короткого основания, и длинной боковой стороны (см. чертёж). Отсюда ясно, что указанная диагональ
прямоугольная, то значит одна из её сторон перпендикулярна основаниям, а другая – наклонная. При этом есть две диагонали: одна идёт из прямого угла в тупой к короткому основанию, а другая – из прямого в острый к длинному основанию. Та диагональ, которая идёт к длинному основанию лежит напротив тупого угла трапеции, а значит она длиннее и короткого основания, и длинной боковой стороны (см. чертёж). Отсюда ясно, что указанная диагональ 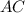 – может быть только диагональю идушей из прямого угла в тупой угол к короткому основанию. В соответствии с этим, расставим названия верщин трапеции
– может быть только диагональю идушей из прямого угла в тупой угол к короткому основанию. В соответствии с этим, расставим названия верщин трапеции 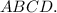 Значит,
Значит, 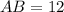 см, а
см, а 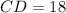 см.
см.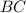 легко найти по теореме Пифагора:
легко найти по теореме Пифагора: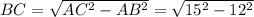 см =
см =  см
см 
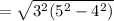 см
см 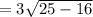 см
см 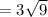 см
см 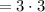 см
см 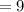 см ;
см ;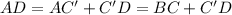 ;
;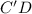 легко найти по теореме Пифагора, учитывая, что
легко найти по теореме Пифагора, учитывая, что 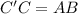 :
: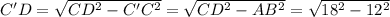 см
см 
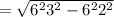 см
см 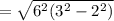 см
см 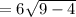 см
см 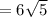 см ;
см ;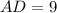 см
см 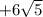 см ;
см ;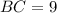 см ;
см ; 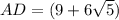 см .
см .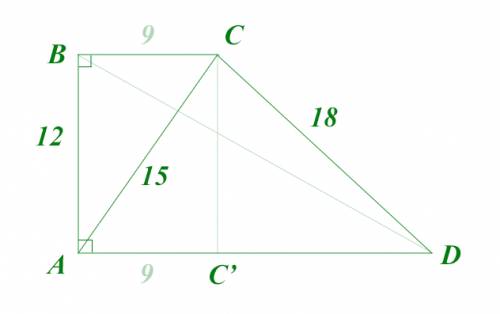
Жумайсынба
20
Объяснение:
АВ=АС значит АВ=13 ВС=24 мы можем узнать чему равно В=12 A=1 C=12
K=8 F=12 ответь
8+12=20