Угол ВОС=2*угол А=2*60=120 (Угол (А), вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом. Величина вписанного угла (А) равна половине центрального угла (ВОС), опирающегося на ту же дугу). АОВ+АОС=360-угол ВОС=360-120=240. АОВ:АОС=3:5 или 5АОВ=3АОС. Обозначим АОВ-х, АОС-у. Составим систему уравнений:
5х=3у 5(240-у)-3у=0 -8у=-1200 у=150 - угол АОС
х+у=240 х=240-у х=240-у х=90 - угол АОВ
Угол С =0,5АОВ=0,5*90=45 (Угол (С), вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом. Величина вписанного угла (С) равна половине центрального угла (АОВ), опирающегося на ту же дугу).
Угол В=0,5АОС=0,5*150=75 (Угол (В), вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом. Величина вписанного угла (В) равна половине центрального угла (АОС), опирающегося на ту же дугу).
))) Интересное задание, сначала не хотел браться, потом "зацепило"...
Смотрим рисунок и вспоминаем свойство касательных:
Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности (вот почему, собственно, центр вписанной в треугольник окружности лежит в точке пересечения биссектрис...).
Пусть точки М, К и О - точки касания окружности со сторонами АВ, ВС и АС, соответственно.
Из свойства касательных следует, что:
Периметр (пока в рассчётах берём именно периметр Р (большая), а не полупериметр р (малая)):
Так как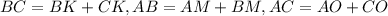 , то:
, то:
Исходя из вышеприведённых равенств:
Имеем право записать как:
В нижней записи у нас уже фигурирует полупериметр р (малая). ЧТД
Как "Лучшее решение" не забудь отметить, ОК?!.. ;)))