а)
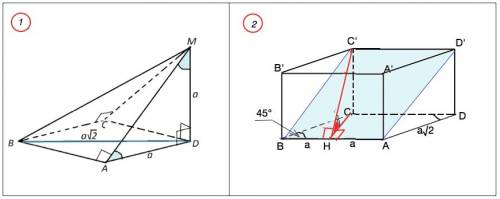
меньшая высота CН параллелограмма ABCD идет из вершины C к большей его стороне АВ.
∆ ВСН - прямоугольный, угол СВН=45° по условию.=>
СН=ВС•sin45°=a√2•√2/2=a
б)
Параллелепипед прямой,⇒ ребро СС’ перпендикулярно плоскости основания и сторонам и является высотой параллелепипеда.
СС’=CH=a
СН перпендикулярна АВ, С'Н⊥АВ по т. о 3-х перпендикулярах
а так как СС’=СH (по условию), треугольник НСС’ равнобедренный прямоугольный.
Угол СНС’ между плоскостью АВС1 и плоскостью основания из равнобедренного прямоугольного треугольника СНС’=45°
в)
Площадь боковой поверхности параллелепипеда равна произведению его периметра на высоту:
S бок=2•( 2а+а√2)•а=4а²+2а²√2=2а²(2+√2)
г)
Площадь поверхности параллелепипеда - сумма площадей 2-х оснований и боковой поверхности.
S (ABCD)=СH•AВ=a•2a=2a²
Оснований два.
S полн=2•2a²+2а²(2+√2)=2а²(4+√2)
я тут уже решал подобную задачу.
Точки пересечения биссектрис - это центры окружностей, касающихся левой (или правой) стороны и обеих оснований. Поэтому отрезок, соединяющий эти центры - ЧАСТЬ СРЕДНЕЙ ЛИНИИ :))). Далее, если бы эти центры совпадали, то длина средней линии была бы равна ПОЛУСУММЕ БОКОВЫХ СТОРОН, то есть 14. (в этом случае трапеция была бы "ОПИСАНА ВОКРУГ ОКРУЖНОСТИ", а у таких 4угольников суммы противоположных сторон равны). Поэтому ответ 21-14=7. :)))
(Именно на это расстояние как бы раздвинуты вписаные окружности - пояснение такое :))).
Еще вариант решения, по сути - такой же
Обе точки пересечения биссектрис лежат на одинаковом расстоянии от оснований, это - центры окружностей, касающихся оснований. Одна касается левого ребра 13, другая - правого 15. Если точки касаний делят верхнее основание на отрезки x, у, z, то сразу ясно, что z - искомое расстояние. И есть 3 соотношения.
z+x+y = b;
z+(13-x)+(15-y) = a;
(a + b)/2 = 21
Складываем и делим на 2.
z = 7