1. Композитор.
2. Известный, великий.
3. Исполняет, сочиняет, вдохновляет.
4. Автор музыкальных произведений.
5. Искусство.
Объяснение:
можно и на последний написать "автор"
Площадь прав тр через радиус вписанной окружности равен 3 корня из 3 на радиус в квадрате, а площадь вписанного круга равна Пи на радиус в квадрате.
Рассмотрим во сколько раз площадь треугольника больше площади круга. ![\frac{3 \sqrt[]{3}r^{2}}{\pi r^{2}}=\frac{3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/07e0a.png)
Пусть площадь круга х, тогда площадь треугольника (по условию) ![x+27\sqrt[]{3}-9\pi](/tpl/images/0144/4450/08b8d.png) с одной стороны и
с одной стороны и ![\frac{x3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/56410.png) с другой.
с другой.
Получим уравнение ![x+27\sqrt[]{3}-9\pi=\frac{x3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/99a9d.png)
Разрешим относительно х. Приведем к знаменателю Пи и приравняем числители
![\frac{x\pi}{\pi}+\frac{\pi27\sqrt[]{3}}{\pi}-\frac{9\pi^{2}}{\pi}=\frac{x3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/4f04e.png)
![x\pi}+\pi27\sqrt[]{3}-9\pi^{2}=x3 \sqrt[]{3}](/tpl/images/0144/4450/57c86.png)
Вынесем 3 корня из трех - Пи за скобки и получим
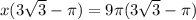
площадь круга = 9Пи
Найдем радиус круга
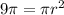
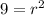
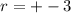
Т к радиус не может быть отрицательным то он равен 3
если треугольник прямоугольный то квадрат самой длиной стороны равен сумме квадратов двух других сторон. 7^2 = 5^2 + 6^2 . 49=25+36. 49=61 неверно, значит треугольник не прямоугольный. Чтобы определить остроугольный он или прямоугольный нужно найти косинус самого большого угла(он лежит против большей стороны).
cosA=(5^2 + 6^2 - 7^2)/2*5*6=12/60=0.2 > 0, значит треугольник остроугольный. Для остальных треугольников поступаем также. Для третьего треугольника 5=3+2 верно, значит треугольник прямоугольный. Для второго треугольника не хватает ещё одной стороны
нет проблем
Объяснение:
нет два ляма в банке