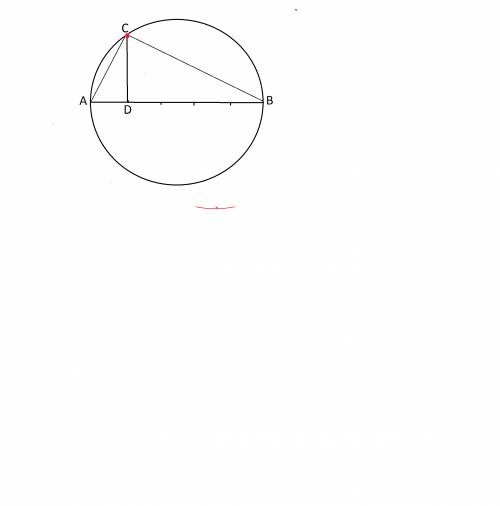
Сделаем рисунок.
АВ - диаметр, АС и СВ - катеты прямоугольного треугольника, поскольку вписанный угол АСВ опирается на диаметр и на дугу 180°, и потому равен 90°.
СD делит диаметр в отношении 1:4, следовательно, на 5 частей - отрезки 1/5 диаметра и 4/5
Диаметр окружности равен 2R =20см
АD=20:5=4 cм
DВ=20-4=16 см
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
DC- высота треугольника АСВ, т.к. по условию это перпендикуляр из С к диаметру, и является расстоянием от С до диаметра.
DC²=АD·DВ=4·16=64
DC=√64=8
Дано:
Треугольник ABC
M ∈ AB
AM = MB
N ∈ BC
BN = NC
MN = 9 см
Найти: AC - ?
Т. к. AM = MB, BN = NC, следовательно MN - средняя линия, следовательно AC = 2MN = 2 × 9 = 18 (см)
ответ: 18 см