
Сфера вписана в цилиндр.
D цилиндра = 10 см
Найти:S полной поверхности цилиндра - S полной поверхности сферы = ?
Решение:D цилиндра = D сферы = 10 см.
=> R цилиндра = R сферы = D/2 = 10/2 = 5 см.
Рассмотрим цилиндр:
S полной поверхности = S боковой поверхности + 2S основания.
S боковой поверхности = 2пRh
S осн = S круга = пR²
h = D
=> S боковой поверхности = п(2 * 5 * 10) = 100п см²
S основания = п * (5)²= 25п см²
=> S полной поверхности = 2 * 25п + 100п = 150п см²
Рассмотрим сферу:
S полной поверхности = 4пR²
S полной поверхности = п(4 * (5)²) = 100п см²
----------------------------------------------------------------------
150п - 100п = 50п см²
ответ: 50п см²
1) 6
2) 17,32
3) 24
Объяснение:
№1
Pi буду писать как П
Sп.п.к. = Sб.п.к. + Sосн.
Sб.п.к. = П * R * L
Sосн. = П *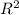
L =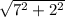 (т.к. треугольник, образованный радиусом, высотой и образующей - прямоугольный) =
(т.к. треугольник, образованный радиусом, высотой и образующей - прямоугольный) = 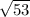
Sб.п.к.= П * 2 *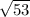 = 2
= 2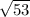 П
П
Sосн. = П *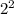 = 4П
= 4П
Sп.п.к. = 2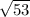 +4 = 6
+4 = 6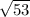
Если нужна целая часть без П, то ответ будет 6, скорее всего
№2
Так как высота перпендикулярна основанию конуса, то высота, радиус и образующая составляют прямоугольный треугольник. Угол равный 30° лежит против катета, равного 10 см. По свойству угла в 30° (угол 30° лежит против катеты, равного половине гипотенузы), гипотенуза = 2*10 = 20 - образующая
По теореме Пифагора найдем радиус
R = =
= 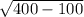 =
= 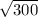
При округлении до сотых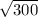 = 17,32
= 17,32
№3
Sо.с.к. = 1/2 * R * H = 1/2 * 8 * 6 = 24