AK=5√6 см, KB=10 см
Объяснение:
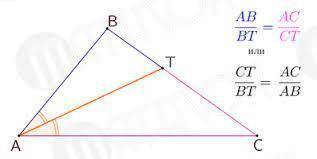
Теорема биссектрисы прикреплена в рисунке. По ней мы имеем:
BK/KC=AB/AC=20/10=2
BK=2KC; CB=BK+KC=15⇒2KC+KC=15
3KC=15; KC=15/3=5 см
BK=BC-KC=15-5=10 см
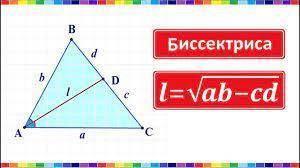
Вторая теорема биссектрисы также прикреплена к ответу. По ней имеем:
AK=√AB*AC-BK*KC=√200-50=√150=√25*√6=5√6
Далее идут доказательства верности ответа другими, тяжёлыми для понимания теоремами. Их не желательно употреблять, они здесь только ради утверждения компетентности моего 2-го ответа. (Ну и для того, чтобы похвастаться знаниями тоже)
Проверим ответ по теореме Стюарта:
AK²*BC=AB²*KC + AC²*BK - BC*KC*BK
AK²*15=400*5 + 100*10 - 15*10*5=2250
AK²=2250/15=150
AK=√150=√25*√6=5√6
ЧТД
Третья формула для нахождения биссектрисы
AK²=AB² * KC/BC + AC² * BK/BC - BK*KC
AK²=2000/15+1000/15-50=200-50=150
AK=√150=√25*√6=5√6
ЧТД
Дано: Δ АВС
∠С = 90°
АК - биссектр.
АК = 18 см
КМ = 9 см
Найти: ∠АКВ
Решение.
Т.к. расстояние от точки измеряется по перпендикуляру, то опустим его из (·) К на гипотенузу АВ и обозначим это расстояние КМ.
Рассмотрим полученный Δ АКМ, Т.к. ∠АМК = 90°,то АК гипотенуза, а КМ - катет. Поскольку, исходя из условия, катет КМ = 9/18 = 1/2 АК, то ∠КАМ = 30°.
Т.к. по условию АК - биссектриса, то ∠САК =∠КАМ = 30°
Рассмотрим ΔАКС. По условию ∠АСК = 90°; а∠САК = 30°, значит, ∠АКС = 180° - 90° - 30° = 60°
Искомый ∠АКВ - смежный с ∠АКС, значит, ∠АКВ = 180° - ∠АКС = 180° - 60° = 120°
ответ: 120°
я мала відповідь але згубила