— 1-е поколение ЭВМ — это ламповые машины 50-х годов.Для ввода программ и данных использовались перфоленты и перфокарты.
— 2-е поколение ЭВМ — транзисторы стали элементарной базой в 60-х годах. ЭВМ теперь надежнее,компактнее, менее энергоемкие.
— 3-е поколение ЭВМ — создано на интегральных схемах.Появляются магнитные диски, новый тип запоминающих устройств.
— 4-е поколение ЭВМ — создан микропроцессор в 1971 году фирмой Intel.Соединив микропроцессор с устройствами внешней памяти,ввода-вывода, изобрели микроЭВМ.
Объяснение:
Дано:
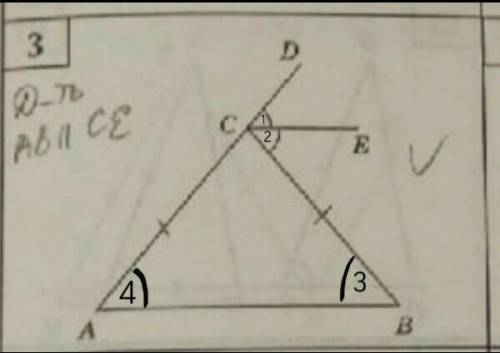
ACB - треугольник.
CE и AB - прямые, пересекающиеся секущими CA и CB.
∠ 1 = ∠ 2;
AC = CB.
Доказать:
AB || CE.
Доказательство:
Вспомним теорему: внешний угол тр-ка равен сумме двух внутренних, не смежных с ним ⇒ ∠ DCB - внешний угол,
а внутренние углы лежат на основании равнобедренного тр-ка ACB (т.к. AC = CB) и в соответствии со свойством (углы при основании в равнобедренном тр-ке равны) можно смело назвать их равными между собой (∠ 3 =∠ 4) т.е. ∠ DCB равен сумме ∠ 3 и ∠ 4 в равнобедренном тр-ке.
CE - биссектриса ∠ DCB ⇒ каждый угол при основании данного равнобедренного тр-ка равен половине внешнего угла DCB ⇒ ∠ 2 = ∠ 3, а они накрест лежащие при прямых CE и AB и секущей CB ⇒ AB || CE (по теореме: если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны)
Также можно отметить, что ∠ 1 = ∠ 4, а они соответственные при прямых CE и AB и секущей CB ⇒ AB || CE (по теореме: если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны).
Доказано!
ΔADC: ∠ADC = 90°, ∠CAD = 30°, ⇒CD = 1/2 AC = 10 / 2 = 5 см, как катет, лежащий напротив угла в 30°.
ΔADC: ∠DCA = 90° - ∠CAD = 60°, так как сумма острых углов прямоугольного треугольника равна 90°.
ΔCDE: ∠CED = 90°, ∠DCE = 60°, ⇒ ∠ CDE = 30°,
тогда СЕ = 1/2 CD = 5/2 = 2,5 см, как катет, лежащий напротив угла в 30°.
АЕ = АС - СЕ = 10 - 2,5 = 7,5 см