Если точка C(x0, y0) делит отрезок с концами в точках A(x1, y1) и B(x2, y2) в отношении 2 : 3, считая от точки A, то по теореме о пропорциональных отрезках проекция точки C на ось OX делит проекцию отрезка AB на эту ось в том же отношении, то есть = ⅔. Отсюда находим, что
x0 = ⅕ (3x1 + 2x2) = (3·(–6) + 2·4) : 5 = –2.
Аналогично y0 = ⅕ (3y1 + 2y2) = (3·1 + 2·6) : 5 = 3.
ответ
(–2, 3).
Источники и прецеденты использования
web-сайт
Название Система задач по геометрии Р.К.Гордина
URL http://zadachi.mccme.ru
задача
Номер 4235
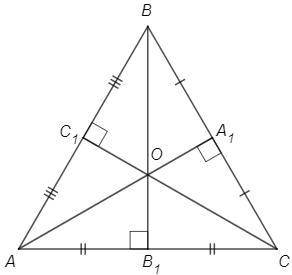
Медианы треугольника пересекаются в одной точке.
Высоты треугольника пересекаются в одной точке.
В данном треугольнике эти точки совпадают - медианы являются также высотами.
Совпадение медианы и высоты к основанию - признак равнобедренного треугольника.
Таким образом данный треугольник является равнобедренным относительно любой стороны, то есть равносторонним.
O - точка пересечения медиан, AA1 - медиана, A1 - середина BC.
O - точка пересечения высот (ортоцентр), AA1 проходит через точку O => AA1 - высота, AA1⊥BC
∠AA1B=∠AA1C=90 (AA1 - высота)
BA1=CA1 (AA1 - медиана)
△BAA1=△CAA1 (по двум катетам, AA1 - общий) => AB=AC
(Доказали: Если медиана треугольника совпадает с его высотой, то треугольник равнобедренный.)
Аналогично: BB1 - медиана и высота к стороне AC => AB=BC
AB=AC=BC, △ABC - равносторонний
Если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды. То есть СМ*МD = АМ*МВ = 36.
Хорда АВ = 5Х (так как делится точкой М на отрезки АМ:МB=4:1), и делится на отрезки АМ=4х и МВ=х. Тогда роизведение этих отрезков равно 4Х*Х=4Х²=36. Отсюда х=3 см. Тогда АМ=12 см, а МВ=3 см. Хорда АВ=АМ+МВ = 12+3=15 см.
ответ: хорда АВ = 15см.