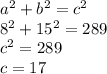
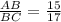 - то и есть коэффициент подобия этих треуг.
- то и есть коэффициент подобия этих треуг.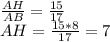
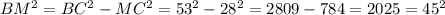 . ВМ=45.
. ВМ=45. , то отношение длин задает отношение центральных углов, которыми данные дуги определены, то есть один центральный угол будет равен 9х, а другой 11х. В сумме они дают 360 градусов, значит: 9х+11х=360, тогда 20х=360, х=18. Центральный угол, опирающийся на меньшую из дуг равен 9х=9*18=162 градуса.
, то отношение длин задает отношение центральных углов, которыми данные дуги определены, то есть один центральный угол будет равен 9х, а другой 11х. В сумме они дают 360 градусов, значит: 9х+11х=360, тогда 20х=360, х=18. Центральный угол, опирающийся на меньшую из дуг равен 9х=9*18=162 градуса.
обозначив высоту цилиндра и диаметр окружности основания цилиндра за х по теореме Пифахора составим уравнение x^2+x^2=(4№2)^2; 2x^2=32; x=4; V=h*Sосн=4*п*4^2=64п