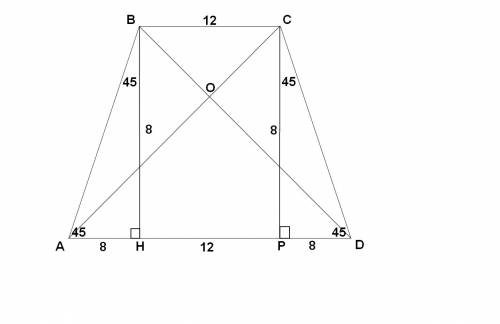
См. рис.
AВ = CD => AВСD - равнобедрая трапеция => А = D = 45° = АВН = РСD =>
=> AD = 28 (см)
а) S=(AD+BC) / 2 * h = (28+12) /2 * 8 = 160 (кв. см)
б) ОАD = OCB, OBC = ODA (т.к. BC || AD) => треуг. АОD и BOC подобны =>
=> k = AD / BC = 28 / 12 = 7 / 3 = 2 + 1/3 (коэфф. подобия)
SAOD / SВОС = k*k = 49 / 9 = 5 + 4 / 9 (отношение площадей подобных треугольников равно квадрату коэфф. подобия)
1. сначала рисуем основание и от одного из его концов, с циркуля, в сторону направления второй стороны, рисуем полукруг, равный по радиусу этой известной стороне.
2. Затем с циркуля с двух концов основания восстанавливаем перпендикуляры к самому основанию (как это делать Вы знаете).
3. С линейки отмеряем известную высоту на обоих перпендикулярах, начиная от основания.
4 Соединяем вершины высот прямой линией с линейки. Полученная линия параллельна основанию.
5. Место пересечения этой линии и полуокружности - это вершина нужного треугольника. Соединим её с концами основания.
6. С циркуля нарисуем второй полукруг к вершине от другого конца основания так, чтобы оба полукруга пересекались сверху и снизу. Соединим точки их пересечения. Получится высота треугольника.
Объяснение:
Решение Вашего задания во вложении