ГЕОМЕТРИЯ 8 КЛАСС №1 В прямоугольном треугольнике ABC с прямым углом C гипотенуза равна 9см, а косинус угла B равен 2\3. Найдите катет BC прямоугольного треугольника.

Задание №2
В треугольник ABC проведена средняя линяя DE. Площадь треугольника ADE равна 28см². Найдите площадь треугольника ABC.

Задание №3
Найдите площадь треугольника ABC, если AB = 8см, BC=6см, AC=4см.

Задание №4
Докажите, что треугольник является прямоугольным, если длины его сторон равны 9,12 и 15см соответственно.

Задание №5
cosA = 3\7. Найдите sinA и tgA.

СДЕЛАЙТЕ 3-4 ЗАДАНИЯ МОЛЮ,

👇

Открыть все ответы

Ответ:

markzastawa

04.06.2022

Пусть E - точка пересечения прямых BC и AD. Если Е не совпадает с D (на чертеже изображен как раз один из таких случаев), то прямоугольные треугольники BED и CED равны по гипотенузе и катету:
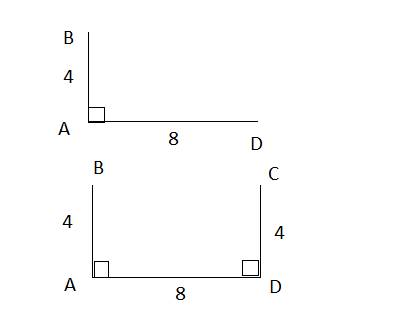
BD=CD по условию, а ED - общий катет. Отсюда ∠BDE=∠CDE,
а т.к. точки A,D,E лежат на одной прямой, то и ∠BDA=∠CDA.
(Заметим, что если Е совпала с D, то равенство углов ∠BDA и ∠CDA следует сразу из условия, т.к. BC⊥AD).
Далее, треугольники BDA и CDA равны по сторонам и углу между ними
(AD - общая, BD=CD по условию, ∠BDA=∠CDA доказали выше), а значит, AB=AC, что и требовалось.

Дано: ad перпендикулярно bc; bd=cd. докажите,что: ab=ac. решите *

Дано: ad перпендикулярно bc; bd=cd. докажите,что: ab=ac. решите *

4,8(52 оценок)

Ответ:

milena162

04.06.2022

1. Рисуем ∠ B =45°. Откладываем отрезки ВА=3 см и АD=7 cм
Через точки В и D проводим паралелльные прямые до пересечения в точке C
2. Рисуем прямой угол A
Откладываем на сторонах угла отрезки равные 4 и 8 см
АВ=4 см
ВD= 8 cм
Проводим перпендикуляр из точки D.
Строим отрезок DC= 4 cм
Соединяем В и С

3, Проводим две взаимно перпендикулярные прямые.
Диагонали ромба взаимно перпендикулярны и делятся в точке пересечения пополам. Откладываем от точки пересечения отрезки 4 и 4 влево и вправо и 2 и 2 вверх и вниз.
См. рисунок
Авсм – параллелограмм, ав = 7см, вс=3см, угол в=45. 2.построить прямоугольник со сторонами 4см и 8см