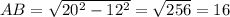 см
см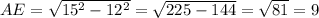 см
см найдём площадь
найдём площадь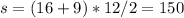 см квадратных
см квадратныхВисота дорівнює 8 см.
Объяснение:
Данний тип задач вирішується дуже просто, навіть устно. Покажу як це робиться в Варшавській школі: одна грань має площу 64 см² а друга 56 см², щоб отримати цю площу треба 8х8=64 , а іншу 7х8=56 , грані це прямокутники , в цих двох виразах є одне спільне, це величина 8 на яку ми множимо сторону основи паралелопипеда. Тому висота дорівнює 8.
Перевіримо: маємо об"єм фігури , в це площа основи * на висоту. Площа основи буде 8*7=56 см² , а висота 8 56*8=448 см³ а це відповідає умовам задачі.
Задачу можна рішати і іншим позначати невідомі сторони через Х і У , складати систему рівнянь , і врешті ми знайдемо це саме, але витратимо на це в тричі більше часу , ніж це я зробив. Удачі всім!
При пересечении параллельных прямых секущей образуется 8 углов двух величин:
соответственные углы
∠1 = ∠5
∠3 = ∠7,
а так как ∠1 = ∠3 как вертикальные, то
∠1 = ∠5 = ∠3 = ∠7 = х
и соответственные углы
∠2 = ∠6
∠4 = ∠8,
а так как ∠2 = ∠4, как вертикальные, то
∠2 = ∠6 = ∠4 = ∠8 = у
Сумма односторонних углов равна 180°, например
∠3 + ∠6 = 180°
Т. е. х + у = 180°.
Углы, о которых идет речь в задаче, не равны. Пусть х - меньший из них, тогда у = х + 30°.
x + x + 30° = 180°
2x = 150°
x = 75°
∠1 = ∠5 = ∠3 = ∠7 = 75°
у = 180° - 75° = 105°
∠2 = ∠6 = ∠4 = ∠8= 105°
Треугольник АСЕ имеет стороны 20 и 15 и высоту к третьей стороне 12. Можно, конечно, тупо сосчитать оба отрезка, на которые высота делит третью сторону, по теореме Пифагора, но тут легко заметить, что это "египетский" треугольник (то есть подобный прямоугольному треугольнику со сторонами 3,4,5) со сторонами 15,20,25 и высотой к гипотенузе 12, его площадь 150.