Нехай маємо прямокутний трикутник ABC (∠C=90), AL – бісектриса, яка проведена до сторони BC, тоді ∠ALC=70 градусів (за умовою).
Побудуємо рисунок трикутника та бісектриси в ньому

У прямокутному ΔALC (∠ACL=90), за теоремою про суму кутів трикутника, знайдемо ∠CAL:
∠CAL=180-∠ACL-∠ALC=180-90-70=20.
За означенням бісектриси AL в трикутнику ΔABC отримаємо:
∠A=2•∠CAL=2•20=40.
У прямокутному ΔABC (∠C=90), за теоремою про суму кутів трикутника, знайдемо ∠B:
∠B=180-∠C-∠A =180-90-40=50
Отже, ∠A=40 – менший гострий кут ΔABC.
Відповідь: 40 градусів.
Приклади на кути трикутника, та й загалом на геометричні фігури слід розв'язувати з побудови допоміжного рисунку (неважна якість, головне намалювати та позначити задані величини); далі виписування, що задано та самого обчислення шуканих величин.
Як тільки навчитеся будувати геометрію, все решта прийде в процесі розв'язування.
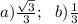
Объяснение:
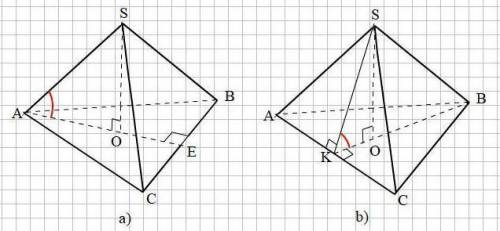
Смотри прикреплённый рисунок.
Пусть а = 8 см - ребро тетраэдра
a) В основании АВС проведём высоту АЕ ⊥ ВС. АЕ = 0,5а√3;
Опустим высоту SO на плоскость АВС.
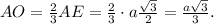
Угол между прямой SA и плоскостью АВС есть угол SAO
b) В основании АВС проведём высоту BK ⊥ AС. BK = 0,5а√3;
Опустим высоту SO на плоскость АВС.
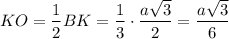
Проведём в грани SAC апофему SK = 0,5а√3
Угол между плоскостями SAC и АВС есть угол SKO между апофемой SK и высотой основания ВК как угол между двумя перпендикулярами, восставленными из точки К к линии пересечения АС плоскостей SAC и АВС
Поскольку тетраэдр правильный, то углы между любой боковой плоскостью и плоскостью основания равны между собой. И косинус между плоскостью SBC и плоскостью АВС равен 1/3.
75 см ²
Объяснение:
Пусть одна диагональ будет 2х см, а вторая 3х см.
Составляем уравнение
2х+3х=25
5х=25
х=25/5
х=5
2*5=10 см первая диагональ.
3*5=15 см вторая диагональ.
S=1/2*d1*d2=1/2*10*15=75см² площадь ромба