Правильное условие задания:
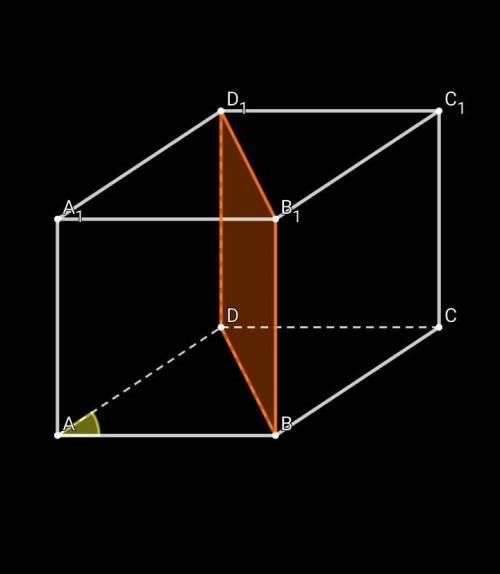
Стороны основания прямого параллелепипеда равны 2 см и 2√3 см, а один из углов основания равен 30 °. Площадь диагонального сечения параллелепипеда, который проходит через меньшую диагональ основания, равен 8 см². Найдите площадь полной поверхности параллелепипеда.
В ΔABD применим теорему косинусов:
BD² = AB² + AD² - 2•AB•AD•cos∠BAD
BD² = 2² + (2√3)² - 2•2•2√3•cos30° = 4 + 12 - 8√3•(√3/2) = 16 - 12 = 4
BD² = 4 ⇒ BD = 2 см
Площадь диагонального сечения: S (bb₁d₁d) = 8 см²
BB₁D₁D - прямоугольник ⇒ S = BD • B₁B = 2 • B₁B = 8 ⇒ B₁B = 4 см
Площадь полной поверхности параллелепипеда:
S (полн.) = 2•S (осн.) + S (бок.) = 2 • S (осн.) + P (осн.) • H = 2•(AB•AD•sin30°) + 2•(AB + AD)•B₁B = 2•(2•2√3•sin30°) + 2•(2 + 2√3)•4 = 4√3 + 16 + 16√3 = 20√3 + 16 cм²
ответ: 20√3 + 16 см²
Косинус - отношение прилежащего катета к гипотенузе.
Тангенс - отношение противолежащего катета к прилежащему.
1)Что значит синус 3/5? Это значит, что противолежащий катет равен 3 см, а гипотенуза равна 5 см. Начертим прямоугольный треугольник и сотрем катет, равный 3 см. Получим искомый угол.
2) То же самое делаем и с косинусом, то есть прилежащий катет будет равен 5, а гипотенуза равна 6 см. Опять же, стоите прямоугольный треугольник с прилежащим катетом 5 см и гипотенузой 6 см. Сотрете неизвестный катет и получите искомый угол.
3) С тангенсом дело будет иначе. Тангенс - отношение противолежащего катета к прилежащему. Строите прямоугольный треугольник. То есть один катет будет равен 2 см, а второй 1 см. Дальше достраиваете гипотенузу и сотрете катет, который равен 2 см.
4) 0.4 = 4/10 = 2/5. То есть в прямоугольном треугольнике противолежащий катет будет равняться 2 см, а гипотенуза 5 см. Достроите второй катет. В итоге получите искомый треугольник с синусов 0,4