Найдем площадь треугольника PKT:
p_{\triangle PKT} = \frac{PK+KT+PT}{2}=\frac{17+65+(30+50)}{2}=\frac{82+80}{2}=\frac{162}{2}=81 \ cmp
△PKT
=
2
PK+KT+PT
=
2
17+65+(30+50)
=
2
82+80
=
2
162
=81 cm
\begin{gathered}S_{\triangle PKT} = \sqrt{p_{\triangle PKT}\cdot (p_{\triangle PKT}\cdot PK)\cdot(p_{\triangle PKT}-KT)\cdot(p_{\triangle PKT}-PT)}= \\ \\ =\sqrt{81\cdot(81-17)\cdot(81-65)\cdot(81-80)}=\sqrt{81\cdot 64\cdot16\cdot 1}=9\cdot8\cdot 4=288 \ cm^2\end{gathered}
S
△PKT
=
p
△PKT
⋅(p
△PKT
⋅PK)⋅(p
△PKT
−KT)⋅(p
△PKT
−PT)
=
=
81⋅(81−17)⋅(81−65)⋅(81−80)
=
81⋅64⋅16⋅1
=9⋅8⋅4=288 cm
2
H=\frac{2S_{\triangle PKT}}{PT}=\frac{2\cdot 288}{80}=\frac{288}{40}=\frac{144}{20}=\frac{72}{10}=7,2 \ cmH=
PT
2S
△PKT
=
80
2⋅288
=
40
288
=
20
144
=
10
72
=7,2 cm
\begin{gathered}S_{\triangle PKC}=\frac{1}{2}\cdot H\cdot PC=\frac{1}{2}\cdot 7,2\cdot 30=\frac{1}{2}\cdot \frac{72}{10}\cdot 30=36\cdot 3 =108 \ cm^2 \\ \\ S_{\triangle KCT}=\frac{1}{2}\cdot H\cdot CT=\frac{1}{2}\cdot 7,2\cdot 50=\frac{1}{2}\cdot \frac{72}{10}\cdot 50=36\cdot 5=180 \ cm^2 \\ \\\end{gathered}
S
△PKC
=
2
1
⋅H⋅PC=
2
1
⋅7,2⋅30=
2
1
⋅
10
72
⋅30=36⋅3=108 cm
2
S
△KCT
=
2
1
⋅H⋅CT=
2
1
⋅7,2⋅50=
2
1
⋅
10
72
⋅50=36⋅5=180 cm
2
дано: δ авс
∠с = 90°
ак - биссектр.
ак = 18 см
км = 9 см
найти: ∠акв
решение.
т.к. расстояние от точки измеряется по перпендикуляру, то опустим его из (·) к на гипотенузу ав и обозначим это расстояние км.
рассмотрим полученный δ акм, т.к. ∠амк = 90°,то ак гипотенуза, а км - катет. поскольку, исходя из условия, катет км = 9/18 = 1/2 ак, то ∠кам = 30°.
т.к. по условию ак - биссектриса, то ∠сак =∠кам = 30°
рассмотрим δакс. по условию ∠аск = 90°; а∠сак = 30°, значит, ∠акс = 180° - 90° - 30° = 60°
искомый ∠акв - смежный с ∠акс, значит, ∠акв = 180° - ∠акс = 180° - 60° = 120°
ответ: 120°
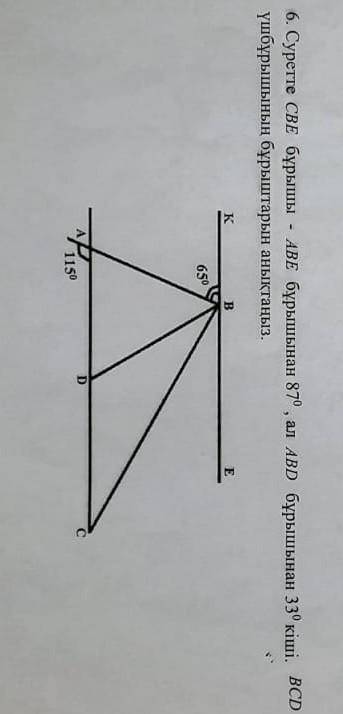
АВЕ=180-65=115
СВЕ=115-87=28
АВD=28+33=61
DBC=180-(61+28+65)=26
DAB=180-115=65
BDC=65+61=126
BCD=180-(26+126)=28
Объяснение:
отметь лучшим