Давайте позначимо точку, що знаходиться на відстані 16 см від прямої, як "P". Також, позначимо точку перетину похилих з прямою як "O", довжину першої похилої як "x", а довжину другої похилої як "y".
За умовою, кути між похилою і прямою складають 30° і 60°. Це означає, що ми маємо справу з 30-60-90 трикутниками. У такому трикутнику, відношення довжин сторін складає:
сторона проти 30° кута : сторона проти 60° кута : гіпотенуза = 1 : √3 : 2.
Тепер, залежно від положення точки "P", варіюються довжини похилих:
Якщо "P" знаходиться в середині гіпотенузи, то перший трикутник буде мати довжини сторін x : x√3 : 2x, і другий трикутник буде мати довжини сторін y : y√3 : 2y.
Якщо "P" знаходиться в межах однієї зі сторін гіпотенузи, то одна з похилих буде містити точку "P" і мати довжини сторін x : x√3 : 2x, а друга похила буде мати довжини сторін y : y√3 : 2y.
А якщо "P" знаходиться за межами гіпотенузи, то обидві похилі будуть мати довжини сторін x : x√3 : 2x і y : y√3 : 2y.
Знаючи це, ми можемо обчислити довжини похилих і їх проекцій на пряму, залежно від положення точки "P". Надайте точніше розташування точки "P", і я надам розрахунки для цього конкретного випадку.

Задача має два розв'язки:
1) якщо трикутник гострокутний, то третя сторона дорівнює 5 см
2) якщо тупокутний, то √137 см, або приблизно 11,7 см
Объяснение:
Уточнена умова:
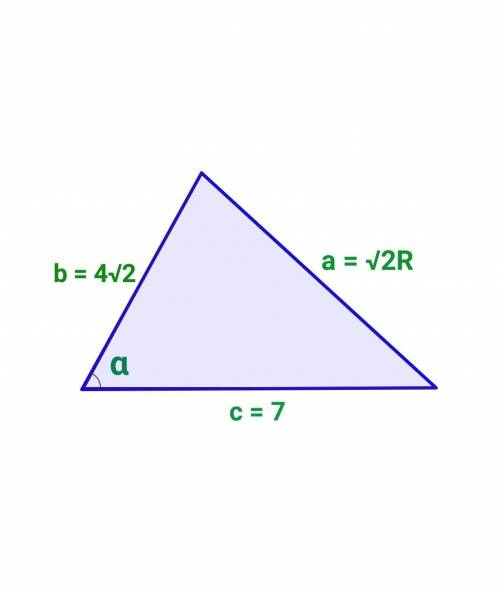
Дві сторони трикутника дорівнюють 4√2 см і 7 см. Знайдіть третю сторону трикутника, якщо вона у √2 разів більша за радіус кола, описаного навколо трикутника. Скільки розвʼязків має задача?
1) За узагальненою теоремою синусів маємо:
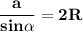
де R - радіус кола, описаного навколо трикутника, а - третя сторона трикутника.
За умовою а=√2R, тоді:
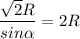
Звідки:
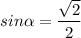
sinα = sin(180°-α).
Отже, якщо:
трикутник гострокутний, то α=45°, якщо тупокутний, то α=135°.2) α=45°.
cos 45° = √2/2
За теоремою косинусів:
а²=b²+c²-2bc•cosα
a²=(4√2)²+7²-2•4√2•7• √2/2 = 32+49-56=25
a=5 (см)
2) α=135°.
cos 135° = cos (180°-45°) = -cos45° = -√2/2
За теоремою косинусів:
а²=b²+c²-2bc•cosα
a²=(4√2)²+7²-2•4√2•7• (-√2/2) = 32+49+56=137
a=√137 ≈ 11,7 (см)
Відповідь: задача має два розв'язки. 5 см або √137 см
#SPJ1
будет 7 сантиметров
Объяснение:
21:3=7