а) (-2;0) - центр окружности, радиус окружности равен 3.
б) (0; 4) - центр окружности, радиус окружности равен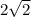 
.
в) (5; -7) - центр окружности, радиус окружности равен 4.
Объяснение:
Уравнение окружности имеет вид: (x-a)²+(y-b)²=R². Здесь центр окружности (a; b) . R - радиус окружности.
а) (-2; 0) -центр окружности, R²=9. R²=3². R=3.
б) (0; 4) - центр окружности,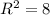 
, 
.
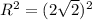
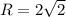в) (5; -7) - центр окружности, R²=16,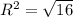 
, R=4.
Заметим, что по условию задачи радиус всегда должен быть положительным. То есть при извлечении корня выбираем только арифметический корень
основание призмы - квадрат
S квадрата = а², а - сторона квадрата
D=25 см
H=15 см
1. прямоугольный треугольник:
гипотенуза D=25 см - диагональ правильной четырехугольной призмы
катет Н = 15 см - высота правильной четырехугольной призмы
катет d - диагональ основания правильной четырехугольной призмы, найти по теореме Пифагора
D²=H²+d²
25²=15²+d², d²=25²-15², d²=625-225. d²=400
2. прямоугольный треугольник:
катет а= катету b
гипотенуза d (диагональ квадрата)
по теореме Пифагора:
a²+a³=d³, 2a²=d²
2a²=400
a²=200, => S квадрата =200 см²
ответ:
площадь основания правильной четырехугольной призмы =200 см²