В трапеции, в которую вписана окружность, суммы противоположных сторон равны a+с=b+d, в этом случае высота является средним геометрическим оснований
h = √b*d = √9*16 = √144 = 12 cм - это диаметр вписанной окружности, а она является вписанной для описанной трапеции.
R = d/2 = 12/2 = 6см
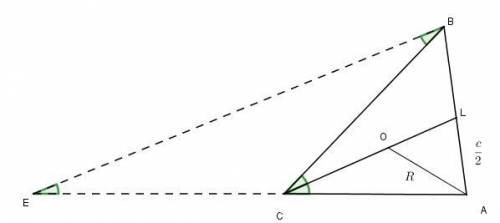
Из вершины В продлим сторону параллельную CL до пересечения продления стороны АС так что EC = BC; ∠ EBD = ∠BCL = α как накрест лежащие при EB || CL и секущей BC.
∠BEC = ∠EBC ⇒ ΔEBC — равнобедренный. Из этого треугольника
EB = 2BC * cosα (высота, проведенная к ЕВ, делит на два равных прямоугольных треугольника, отсюда и легко найти).
ΔCLA ~ ΔEBA следовательно из подобия 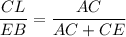
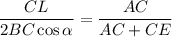
BC = CE, тогда
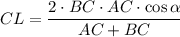
Среднее гармоническое двух чисел a;b : 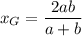 , а среднее геометрическое -
, а среднее геометрическое - ![x_{GEOM}=\sqrt[]{ab}](/tpl/images/0375/1324/773ff.png) .
. 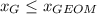 . В данном случае достигает максимума, когда выполняется равенство а=b.
. В данном случае достигает максимума, когда выполняется равенство а=b.
Т.к. α — постоянная величина ; среднее гармоническое не превосходит среднего геометрического и достигает максимума , тогда и только тогда, когда AC=BC , а значит треугольник равнобедренный, отсюда CL - высота и медиана
По т. Пифагора из треугольника OLA:
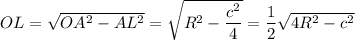
OC = OA = R, окончательно имеем:
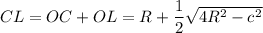
боковая сторона (9+16)/2=12,5
(2R)^2=12,5^2-3,5^2=12
R=12/2=6