RS || MQ
MR || SQ
Объяснение:
Рассмотрим прямые RS и МQ. Они равны по условию, а также ∠RSM=∠SMQ как внутренние разносторонние – по условию. Эти углы всегда равны если параллельные прямые пересекает секущая. Следовательно RS || MQ
Рассмотрим ∆RSM и ∆SMQ. У них:
1) RS=MQ - по условию
2) ∠RSM=∠SMQ – по условию
3) MS –общая сторона
Эти треугольники равны по первому признаку – по двум сторонам и углу между ними, соответственно RM=SQ, следовательно этот четырёхугольник параллелограмм, у которого противоположные стороны равны и параллельны
ДОКАЗАНО
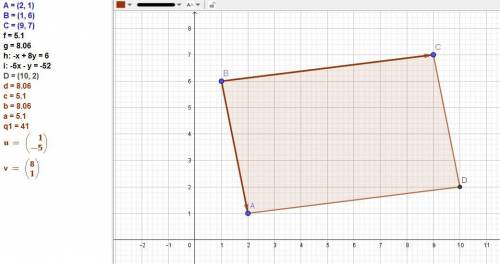
Площадь параллелограмма равна модулю векторного произведения векторов, выходящих из одной вершины.
Вектор ВА = (1; -5),
вектор ВС = (8; 1).
S = |a × b|
Найдем векторное произведение векторов:
c = a × b
a × b =
i j k
ax ay az
bx by bz
=
i j k
-1 5 0
8 1 0
= i (5·0 - 0·1) - j ((-1)·0 - 0·8) + k ((-1)·1 - 5·8) =
= i (0 - 0) - j (0 - 0) + k (-1 - 40) = {0; 0; -41}
Найдем модуль вектора:
|c| = √(cx² + cy² + cz²) = √(0² + 0² + (-41)²) = √(0 + 0 + 1681) = √1681 = 41.
Найдем площадь параллелограмма:
S = 41.
В самом деле, треугольники, образованные диагоналями и основаниями, очевидно подобны, то есть их стороны относятся, как основания. Раз диагонали равны, то равны и отрезки этих диагоналей от вершин до точки пересечения, то есть это равнобедренные треугольники, с равными улами при основаниях, а это означает, что треугольники, образованные (например) большим основанием, боковой стороной и диагональю, равны по двум сторонам и углу между ними.
Поэтому трапеция, у которой диагонали равны - равнобедренная.
Раз так, то отрезок, соединяющий середины оснований - это попросту высота, по условию это 8. Отрезок, соединяющий середины боковых сторон - это средняя линяя, она равна 8.
Остается найти длину отрезков, соединяющих середины соседних сторон. Для этого надо найти длину диагонали.
Проводится высота из вершины малого основания, получается прямоугольный треугольник с катетами 8 (это высота) и 8 - это часть большого основания. В самом деле, от ближайшего конца большого основания до конца проведенной высоты
(9 - 7)/2 = 1, поэтому до другого конца 9 - 1 = 8.
Диагональ - гипотенуза в этом треугольнике, она равна 8*корень(2).
Длина отрезка, соединяющего середины соседних сторон, равна половине диагонали - как средняя линяя в треугольнике, образованном диагональю и двумя сторонами трапеции. То есть она равна 4*корень(2).
Ясно, что такая длина у всех четырех отрезков, соединяющих середины любой пары соседних сторон. Поэтому эти отрезки образуют ромб. Однако в данной задаче это не просто ромб, а квадрат, поскольку высота равна средней линии. :)