192см²
Объяснение:
Дано
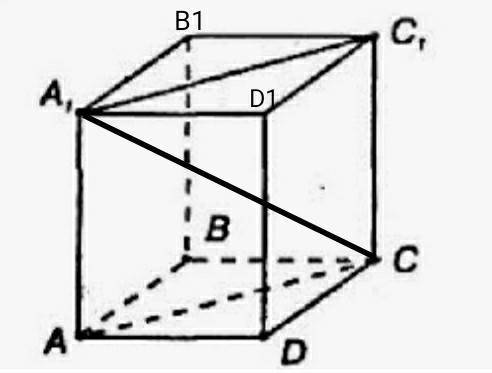
ABCDA1B1C1D1 - параллелепипед
AD=4см
DC=12cм
А1С=13 см.
Sпол=?
Решение.
∆ADC- прямоугольный
По теореме Пифагора найдем гипотенузу
АС²=АD²+DC²=4²+12²=16+144=160 см
AC=√160 см
∆АА1С- прямоугольный.
По теореме Пифагора найдем катет
АА1=А1С²-АС²=13²-(√160)²=169-160=9
АА1=√9=3см.
Sбок=Рaвсd*AA1
Paвсd=2*4+2*12=8+24=32 см периметр прямоугольника АВСD.
Sбок=32*3=96см². площадь боковой поверхности параллелепипеда
Sосн=АD*DC=4*12=48 см² площадь прямоугольника ABCD.
Sпол=2*Sосн+Sбок=2*48+96=192 см² площадь полной поверхности параллелепипеда.
1. ΔАВС и ΔАDС равны по второму признаку равенства треугольников. в них АС- общая. а углы, прилежащие к этой стороне, равны по условию. Поэтому АВ=DС, ВС=АD, значит, по признаку параллелограмма четырехугольник АВСD - параллелограмм. Доказано.
5. BD- общая для ΔАВD и ΔDСВ, стороны ВС и АD -равны по условию, углы между ВD и ВС и ВD и DА равны по условию. значит, ΔАВD и ΔDСВ равны по первому признаку равенства треугольников. а ВС и АD равны и параллельны, т.к. ∠СВD=∠АDВ, а это внутренние накрест лежащие при ВС и АD и секущей ВD, по признаку четырехугольник АВСD - параллелограмм. Доказано.
7. Из равенства этих треугольников вытекает равенство сторон АВ и С D , кроме того, углы ВАО и СОD равны, но это внутренние накрест лежащие при прямых АВ и СD, секущей АС, значит, прямые АВ ║ СD.
По признаку четырехугольник АВСD - параллелограмм. Доказано.