Провели несколько измерений случайной величины: 6,18,17,14,4,22,18.найдите моду этого набора чисел

👇

Увидеть ответ

Ответ:

avritsevich0116

20.10.2022

отсортируем ряд 4 ; 6; 14; 17; 18; 18; 22 модой будет являтся число 18

4,4(73 оценок)

Ответ:

NeviL1488

20.10.2022

мода - наиболее часто встречющееся число. А если их несколько то их среднее арфиметическое. В данном случае мода равна 18

4,5(48 оценок)

Открыть все ответы

Ответ:

Demongirl1

20.10.2022

Задача 2.

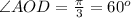
$\angle{AOD} = \frac{\pi}{3} = 60^{o}$

Задача 3.

Проекциями прямых параллельных сторонам исходного параллелограмма будут прямые, проходящие через т. пересечения диагоналей и середины сторон у параллелограмма проекции

Объяснение:

Дано

АВСД - прямоугольник

АВ = 6 см

АД = 2√3 см

Найти

уг. м/ду АС и ВД

Решение

Очевидно, что АС и ВД - диагонали прямоугольника.

Обозначим т. пересечения как т. О

Тогда уг.АОД - искомый угол между диагоналями.

Обозначим

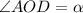
${\angle AOD} = \alpha$

По св-вам прямоугольника, его диагонали равны и в т. пересечения делятся пополам. Т.е.

АО = ОС = ВО = ОД

По Т. Пифагора можно найти диагонали:

ВД² = АВ² + АД²

BD = \sqrt{AB^2 + AD^2} \\ BD = \sqrt{6^2 + 2\sqrt(3)^2}

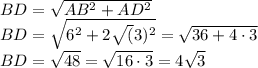
$BD = \sqrt{AB^2 + AD^2} \\ BD = \sqrt{6^2 + 2\sqrt(3)^2} = \sqrt{36 + 4 \cdot3} \\ BD = \sqrt{48} = \sqrt{16\cdot3} = 4 \sqrt{3}$

Соответственно

АС = ВД = 4√3

Рассмотрим тогда треугольник АОД, он равнобедренный, т.к.

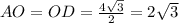
$AO = OD = \frac{4\sqrt3}{2} = 2 \sqrt{3}$

Так же 2√3 равна и сторона АД нашего прямоугольника.

То есть - мы получаем, что

АО = ОД = АД = 2√3

Следовательно - ∆АОД равносторонний,

а это означает, что искомый угол AOД

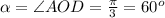
$\alpha = \angle{AOD} = \frac{\pi}{3} = 60^{o}$

Для особо дотошных:

По Т. косинусов имеем:

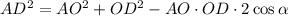
$\small {AD^2=AO^2+OD^2-AO\cdot OD \cdot 2\cos{ \alpha}}$

Отсюда

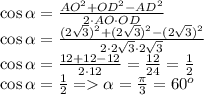
${\cos{ \alpha} = \frac {AO^2+OD^2-AD^2}{2 \cdot AO\cdot OD }} \\ {\cos{ \alpha} = \frac {(2 \sqrt{3})^2 +(2 \sqrt{3})^2 -(2 \sqrt{3})^2 }{2 \cdot 2 \sqrt{3} \cdot 2 \sqrt{3} }} \\ { \cos \alpha = \frac {12 + 12 - 12}{2 \cdot12}} = \frac{12}{24} = \frac{1}{2} \\ \cos \alpha = \frac{1}{2} = \alpha = \frac{\pi}{3} = 60^{o}$

4,5(13 оценок)

Ответ:

yulyatalko

20.10.2022

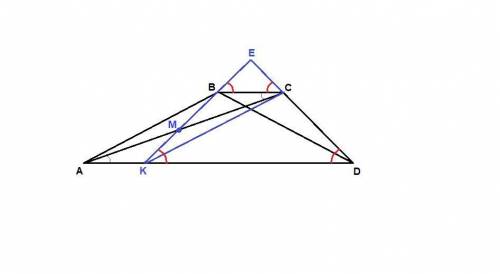
В трапеции ABCD боковая сторона AB равна диагонали BD. Точка M - середина диагонали AC. Прямая BM пересекает прямую CD в точке E. Докажите, что BE = CE.

Объяснение:

К - точка пересечения прямой ВМ с основанием AD.

Рассмотрим треугольники АМК и СМВ:

АМ = МС по условию,

∠АМК = ∠СМВ как вертикальные,

∠МАК = ∠МСВ как накрест лежащие при пересечении параллельных прямых АК и ВС секущей АС, ⇒

ΔАМК = ΔСМВ по стороне и двум прилежащим к ней углам.

Следовательно, АК = ВС.

Если в четырехугольнике две противолежащие стороны равны и параллельны, то это параллелограмм.

Значит, АВСК параллелограмм. ⇒ СК = АВ.

АВ = BD по условию, ⇒ СК = BD.

В трапеции KBCD диагонали равны, значит она равнобедренная.