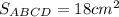все остальные углы нетрудно найти из выражения 165 + n*90, где n - целое
n = 0, угол = 165 + 0*90 = 165 - наш заданный угол
n = 1, угол = 165 + 1*90 = 255 - больше 180 (развернутого угла), т.е. не считается, так же как и для всех n>0, так что переходим в область отрицательных чисел
n = -1, угол = 165 - 1*90 = 75 - острый, не годится, по условию
n = -2, угол = 165 - 2*90 = -15 - так-же острый, не годится
n = -3, угол = 165 - 3*90 = -105 - как раз тупой и меньше чем 165
n = -4, угол = 165 - 4*90 = -195 - по абсолютному значению опять превышает 180 - не годится как и все прочие при n<-4
Так что перебором нашли что меньший тупой гол равен 105 градусам.
все остальные углы нетрудно найти из выражения 165 + n*90, где n - целое
n = 0, угол = 165 + 0*90 = 165 - наш заданный угол
n = 1, угол = 165 + 1*90 = 255 - больше 180 (развернутого угла), т.е. не считается, так же как и для всех n>0, так что переходим в область отрицательных чисел
n = -1, угол = 165 - 1*90 = 75 - острый, не годится, по условию
n = -2, угол = 165 - 2*90 = -15 - так-же острый, не годится
n = -3, угол = 165 - 3*90 = -105 - как раз тупой и меньше чем 165
n = -4, угол = 165 - 4*90 = -195 - по абсолютному значению опять превышает 180 - не годится как и все прочие при n<-4
Так что перебором нашли что меньший тупой гол равен 105 градусам.
Дано:
Розв'язання:
1) Якщо провести відрізки BM та CM, то утворяться два подібні трикутники BMC та AMC за двома кутами (кут М - спільний, а кут D = куту MCB, бо кут BCD + кут D = кут BCD + кут MCB = 180). У подібних трикутниках відношення сторін дорівнює відношенню площ.
2)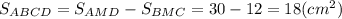
Відповідь: