При пересечении параллельных прямых секущей образуется 8 углов двух величин:
соответственные углы
∠1 = ∠5
∠3 = ∠7,
а так как ∠1 = ∠3 как вертикальные, то
∠1 = ∠5 = ∠3 = ∠7 = х
и соответственные углы
∠2 = ∠6
∠4 = ∠8,
а так как ∠2 = ∠4, как вертикальные, то
∠2 = ∠6 = ∠4 = ∠8 = у
Сумма односторонних углов равна 180°, например
∠3 + ∠6 = 180°
Т. е. х + у = 180°.
Углы, о которых идет речь в задаче, не равны. Пусть х - меньший из них, тогда у = х + 30°.
x + x + 30° = 180°
2x = 150°
x = 75°
∠1 = ∠5 = ∠3 = ∠7 = 75°
у = 180° - 75° = 105°
∠2 = ∠6 = ∠4 = ∠8= 105°
Sбок=(Pосн*h)/2
1) ΔМОК: ∠О=90°, ∠К=45° ⇒ ∠М=45°
МО=ОК=2
МК=2√2=h апофема
2) КО=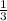 КС
КС
2 = 1/3 КС ⇒ КС = 6 - медиана в ΔАВС
3) m= (a√3)/2=6
а = (6*2)/√3
а=(12*√3)/3 = 4√3 ( сторона основания ΔАВС )
4) Sбок=(3*4√3*2√2)/2=12√6
ответ: S/√6=12√6/√6=12