а) Возьмем угол С прямой. Получим теорему Пифагора, косинус прямого угла равен нулю. а=3, в=4, с=5.
Можно взять угол С тупой, тогда срабатывает теорема косинусов, при условии выполнения неравенства треугольников такой треугольник будет существовать.
ответ Существует.
б) Отношение а к с равно отношению косинуса А к косинусу С. Возьмем, например, угол А и угол С по 45°, а угол В прямой. Тогда при выполнении неравенства треугольников такой треугольник прямоугольный равнобедренный существует.
в) Если угол В прямой, а угол А равен 30°,
сторона с =а√3, в=2а
ответ Существует
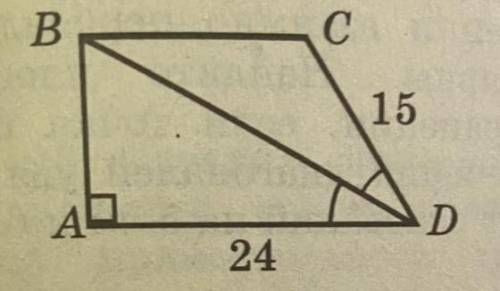
234 ед²
Объяснение:
<АDB=<BDC, по условию.
<ADB=<DBC, углы накрест лежащие
∆ВСD- равнобедренный треугольник, углы при основании равны. ВС=СD.
BC=15
KD=AD-BC=24-15=9
∆KCD- прямоугольный треугольник.
По теореме Пифагора
СК=√(CD²-КD²)=√(15²-9²)=√(225-81)=√144=
=12
S=CK(AD+BC)/2=12(24+15)/2=12*39/2=234