Координаты AB(-1; -3; 2)
Координаты AC(-2; -1; -4)
\begin{gathered}cos\alpha = \frac{|x_{1}x_{2} + y_{1}y_{2} + z_{1}z_{2}|}{\sqrt{x^{2}_{1} + y^{2}_{1} + z^{2}_{1}} + \sqrt{x^{2}_{2} + y^{2}_{2} + z^{2}_{2}}}\\cos\alpha = \frac{3*(\sqrt{21} - \sqrt{14})}{7}\\\alpha = \frac{+}{-}arccos(\frac{3*(\sqrt{21} - \sqrt{14})}{7}) + 2\pi k\end{gathered}
cosα=
x
1
2
+y
1
2
+z
1
2
+
x
2
2
+y
2
2
+z
2
2
∣x
1
x
2
+y
1
y
2
+z
1
z
2
∣
cosα=
7
3∗(
21
−
14
)
α=
−
+
arccos(
7
3∗(
21
−
14
)
)+2πk
Все грани прямоугольного параллелепипеда - прямоугольники.
Двугранный угол DABD₁ - это угол между плоскостями DAB и ABD₁.
АВ - ребро двугранного угла.
DA⊥AB как стороны квадрата,
DA - проекция наклонной D₁A на плоскость DAB, значит
D₁A⊥АВ по теореме о трех перпендикулярах.
DA⊥AB и D₁A⊥АВ,, значит ∠D₁AD - линейный угол двугранного угла D₁ABD.
ΔADC: ∠ADC = 90°, по теореме Пифагора
AD = √(AC² - CD²) = √(100 - 36) = √64 = 8 дм
ΔD₁AD: ∠D₁DA = 90°, DD₁ = AA₁ = 8√3 дм, AD = 8 дм,
tg∠D₁AD = D₁D / AD = 8√3 / 8 = √3
∠D₁AD = 60°
вика
Две плоскости называются взаимно перпендикулярными, если они образуют прямые двугранные углы.
Объяснение:
Возможны три случая взаимного расположения прямой и плоскости в стереометрии:
Прямая лежит в плоскости (каждая точка прямой лежит в плоскости).
Прямая и плоскость пересекаются (имеют единственную общую точку).
Прямая и плоскость не имеют ни одной общей точки.
Определение: Прямая и плоскость называются параллельными, если они не имеют общих точек. Если прямая а параллельна плоскости β, то пишут:
Обозначение параллельности прямой и плоскости
Теоремы:
Теорема 1 (признак параллельности прямой и плоскости). Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
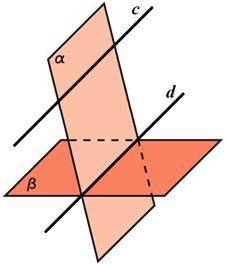
Теорема 2. Если плоскость (на рисунке – α) проходит через прямую (на рисунке – с), параллельную другой плоскости (на рисунке – β), и пересекает эту плоскость, то линия пересечения плоскостей (на рисунке – d) параллельна данной прямой: ( КАРТИНКА )
Если две различные прямые лежат в одной плоскости, то они либо пересекаются, либо параллельны. Однако, в пространстве (т.е. в стереометрии) возможен и третий случай, когда не существует плоскости, в которой лежат две прямые (при этом они и не пересекаются, и не параллельны).
ответ:6
Объяснение:получим:
|AB−→−|=(−4)2+42+22−−−−−−−−−−−−−√=16+16+4−−−−−−−−−√=36−−√=6
ответ. |AB−→−|=6