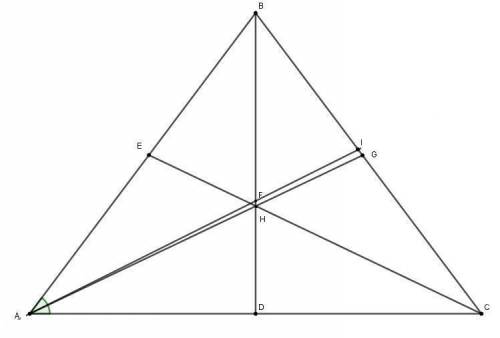
Точка F - точка пересечения биссектрисы угла при основании и высоты BD, H - точка пересечения медиан и делятся этой точкой на две части в отношении 2:1, считая от вершины.
HD = 5 см, следовательно BH = 2 * 5 = 10 см. Высота равнобедренного треугольника BD = 5 + 10 = 15 см.
Из условия BF/FD = 5/4 , пусть BF = 5x, тогда FD = 4x. Тогда по свойству биссектрисы для треугольника ABD
AB/AD = BF/FD = 5/4 ⇒ AB = 5y и AD = 4y
По теореме Пифагора из прямоугольного треугольника ABD
25y² = 16y² + 15²
9y² = 225
y = 5
Следовательно, AB = BC = 25 см и AC = 2*AD = 40 см.
Периметр ΔABC: P = AB + BC + AC = 25+25+40 = 90 см
ответ: 90 см.
Объяснение:
Соединим А и В, С и D. Четырехугольник ABCD - вписанный, значит <ABC+<ADC=180° и <CDM+<ADC=180°, значит <ABC=<CDM. Аналогично <BAD=<DCM.
Из тр-ка △CMD <CMD(AMB)=180-<CDM-<DCM=180-<ABC-<BAD
<ABC=1/2*(AD+CD); <BAD=1/2(BC+CD).
<AMB=180-1/2*(AD+CD)-1/2*(BC+CD)=180-1/2*(AD+CD+BC)-1/2*CD
Для дуг окружности можно записать:
AD+CD+BC=360-AB - подставим в последнее выражение:
<AMB=180-1/2*(360-АВ)-1/2*СD=180-180+1/2*АВ-1/2*СD=1/2*(AB-CD)=1/2*(ALB-CKD)