Верно.
Объяснение:
Это признак параллельности прямой и плоскости:
Если прямая, не лежащая в плоскости, параллельна прямой, лежащей в плоскости, то она параллельна и самой плоскости.
Доказательство:
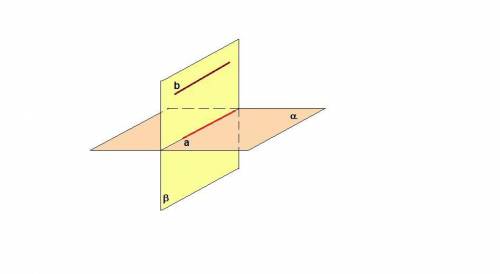
Пусть прямая b параллельна прямой а, лежащей в плоскости α. Докажем, что прямая b параллельна плоскости α.
Через две параллельные прямые можно провести единственную плоскость. Проведем плоскость β через прямые а и b.
Так как прямая а лежит в двух плоскостях, то она является линией пересечения плоскостей.
Предположим, что прямая b не параллельна плоскости α, т.е. пересекает ее. Тогда точка пересечения лежит на прямой а (на линии пересечения плоскостей), но тогда b пересекает прямую а, а это противоречит условию.
Значит b║α. Что и требовалось доказать.
1. Касательные проведнные с одной точки равны между собой, поэтому
AC = AB = 12 см.
По теореме Пифагора
AO=корень(CO^+AC^2)=корень(9^2+12^2)=15 см
ответ: 12 см, 15 см
2. Извини, но незнаю
3. Хорды MN и PK пересекаются в точке E так, что ME = 12 см, NE = 3 см, PE = KE. Найдите PK.
По свойству хорд
ME*NE=PE*KE
Пусть PE = KE=х см
Тогда x^2=12*3=36
x>0, поєтому х=6 см
PK=PE+KE=6см+6см=12 см
ответ:12 см
4.Треугольник ОАВ равнобедренный, ОА=ОВ=16 см (радиусы);
∠А=∠В=30° - по условию;
ОН - высота ОАВ, равна 16/2=8 см (катет против угла 30°);
АВ=2*АН=2*√(16²-8²)=16√3 см.
Треугольник СОВ равнобедренный, ОС=ОВ=16 см (радиусы);
∠С=∠В=45° ⇒ ∠О=90° - прямоугольный ⇒ СВ=√(16²+16²)=16√2 см.
АВ=16√3 см;
ВС=16√2 см.