Дано:
AD-BC=8см
AB+CD=10см
sin a-?
cos a-?
tg a-?
Решение
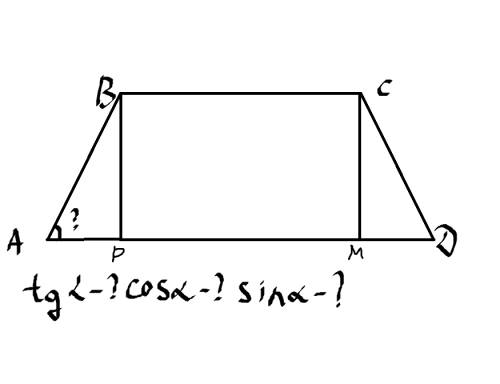
1) Проведем перпиндекуляры из углов B и C к основанию AD
2) Т.к. по условию AD-BC=8 см, то AP+MD+PM-BC=8 см
3) Рассмотрим треугольники ABP и CMD. Они равны по 1 признаку:
1) BP=CM (как перпендикуляры проведенные из равных по величине углов)
2) угол A=D (как углы при основании равнобедренной трапеции)
3) AB=CD (как стороны равнобедренной трапеции)
4) Т.к. треугольники ABP и CMD равны, то AP=MD. Т.к. BC=PM, AP=MD то
AP+MD+PM-BC=8 см
2AP=8 см
AP=4 см
5) AB+CD=10 см - по условию
Т.к. стороны равнобедренной трапеции равны, то
2AB=10 см
AB=5 см, следовательно и CD=5 см
6) Т.к. AB=5 см, AP=4 см, то по теореме Пифагора:
BP=корень (AB^2-AP^2)=корень (25-16)=3 см
7) sin a= BP\AB=3\5=0,6 (синус-отношение противолеж. катета к гипотенузе)
cos a= AP\AB=4\5=0,8 (косинус-отношение прилежащего катета к гипотеннузе)
tg a= BP\AP=0,75 (тангенс-отношение противолеж. катета к прилежащему)
ответ: sin a=0,6 ;cos a=0,8 ;tg a=0,75.
Дано:
AD-BC=8см
AB+CD=10см
sin a-?
cos a-?
tg a-?
Решение
1) Проведем перпиндекуляры из углов B и C к основанию AD
2) Т.к. по условию AD-BC=8 см, то AP+MD+PM-BC=8 см
3) Рассмотрим треугольники ABP и CMD. Они равны по 1 признаку:
1) BP=CM (как перпендикуляры проведенные из равных по величине углов)
2) угол A=D (как углы при основании равнобедренной трапеции)
3) AB=CD (как стороны равнобедренной трапеции)
4) Т.к. треугольники ABP и CMD равны, то AP=MD. Т.к. BC=PM, AP=MD то
AP+MD+PM-BC=8 см
2AP=8 см
AP=4 см
5) AB+CD=10 см - по условию
Т.к. стороны равнобедренной трапеции равны, то
2AB=10 см
AB=5 см, следовательно и CD=5 см
6) Т.к. AB=5 см, AP=4 см, то по теореме Пифагора:
BP=корень (AB^2-AP^2)=корень (25-16)=3 см
7) sin a= BP\AB=3\5=0,6 (синус-отношение противолеж. катета к гипотенузе)
cos a= AP\AB=4\5=0,8 (косинус-отношение прилежащего катета к гипотеннузе)
tg a= BP\AP=0,75 (тангенс-отношение противолеж. катета к прилежащему)
ответ: sin a=0,6 ;cos a=0,8 ;tg a=0,75.

72√3+432
Объяснение:
Дано:
ABCA1B1C1- треугольная призма
АВ=ВС=АС
S(ABC)=36√3
AA1=12
Sпол=?
Решение
Формула нахождения площади равностороннего треугольника
S=a²√3/4, где а-сторона треугольника.
S(ABC)=AB²√3/4
AB=√(4*S(ABC)/√3)=√(4*36√3/√3)=12 сторона треугольника.
Росн=3*АВ=3*12=36 периметр основания
Sбок=Росн*АА1=36*12=432
Sпол=2*S(ABC)+Sбок=2*36√3+432=
=72√3+432.