С РИСУНКОМ
Боковое ребро прямой треугольной призмы равно 12 см, её основание — прямоугольный треугольник, катеты которого равны 3 см и 4 см. Найдите площадь полной поверхности призмы.
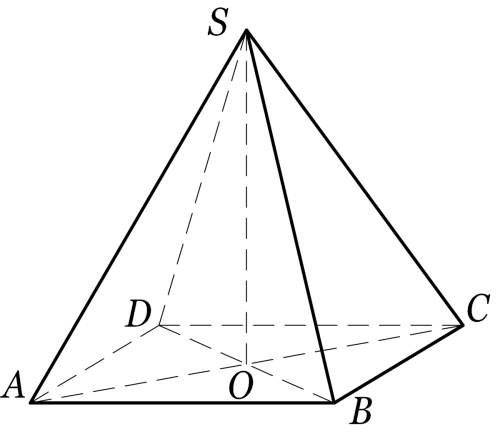
2. Сторона основания правильной четырёхугольной пирамиды равна 2 см, а высота пирамиды — см. Найдите:
1) боковое ребро пирамиды;
2) площадь боковой поверхности пирамиды.
Следовательно, отрезок ВМ=4.
В треугольнике АВС по теореме косинусов: "Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними"
Cosα = (b²+c²-a²)/2bc. (угол α - между b и c). В нашем случае:
CosВ=(64+49-36)/2*8*7=11/16. Формула приведения: Sin²α+Cos²α=1.
Тогда SinВ=√(1-121/16²)=√135/16.
Площадь треугольника АВМ
Sabm=(1/2)*АВ*ВМ*SinB=(1/2)8*4*√135/16=√135.
ответ: Sabm=√135.