1. АВ=√(8²+(-6)²+10²)=10√2
алгоритм - от координат конца отрезка отняли координаты начала. результаты возвели в квадрат, сложили и извлекли корень квадратный из суммы.
2) х=1; у=-1;z=1
алгоритм: сложили соответствующие координаты и поделили каждую на два.
2. 1)АВ(9;-10;7), СВ(4;2;-3) алгоритм : от координат конца отняли координаты начала вектора.
2)IАВI=√(9²+(-10)²+7²)=√230
3) 2АВ+3СВ=2*(9;-10;7)+3(4;2;-3)=(30;-14;5)
2АВ-3СВ=2*(9;-10;7)-3(4;2;-3)=(60;-26;23)
4) IСВI=√(16+4+9)=√29; АВ*СВ/(IАВI*IСВI)=
(36-20-21)/(√230*√29)=-5/√6670≈-5/81.67-0.0612
3. а)-15х-48-27=0⇒х=75/(-15)=-5 скалярное произведение равно нулю.
б)х/(-15)= -4/12= 3/(-9) соответствующие координаты пропорциональны х=5
площадь полной поверхности = площади боковой поверхности + 2 площади основания.
1) в оснвоании лежит прямоугольный треугольник. площадь находим как 1/2 произведения катетов , т..е 12*5: 2= 30 см^2/
2)площадь бококвой поверхности = половине периметра основания на высоту.
чтобы найти периметр , надо знать все три стороны треугольника. треугольник прямоугольный, поэтому гипотенузу находим по теореме пифагора. 12^2+5^2=144+25=169, гипотенуза равна 13.
3) ищем периметр 13+12+5=30 см.
4) ищем площадь боковой поверхности 30*10=300
5) площадь полной поверхности равна 300+2*30=360 см
подробнее - на -
S =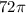
Объяснение:
Во вложении