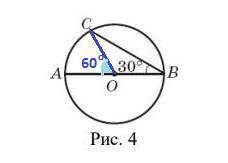
Если диаметр окружности с центром в точке О образует с хордой ВС угол 30°, то
А. треугольник СОВ - равносторонний - НЕ ВЕРНО
В равностороннем треугольнике все углы по 60°, а в треугольнике СОВ ∠В=30°.
Б. ∠ОСВ = 30° - ВЕРНО
В треугольнике СОВ равны две стороны : ОВ=ОС - это радиусы окружности. Значит, ΔСОВ равнобедренный. В равнобедренном треугольнике углы при основании равны : ∠ОСВ=∠В=30°
В. ∠СОА = 50° - НЕ ВЕРНО
∠СОА - внешний угол треугольника ОСВ равен сумме двух внутренних углов, не смежных с ним :
∠СОА = ∠ОСВ + ∠В = 30° + 30° = 60°
ответ : Б, ∠ОСВ = 30°
Центр вписанной окружности является точкой пересечения биссектрис углов трапеции.
1) ∠ADC+∠BCD=180º (как сумма внутренних односторонних углов при параллельных прямых AD и BC и секущей CD);
2) так как точка O — точка пересечения биссектрис углов трапеции, то ∠ODF+∠OCF=1/2∙(∠ADC+∠BCD)=90º;
3) так как сумма углов треугольника равна 180º, то в треугольнике COD ∠COD=90º;
4) таким образом, треугольник COD прямоугольный, а OF — высота, проведенная к гипотенузе, CF и FD — проекции катета OC и OD на гипотенузу.
5) треугольник СОD (по теореме Пифагора):
CD^2 = CO^2 + OD^2
CD = корень [CO^2 + OD^2] = корень [3^2 + 4^2] = 5
6) Обозначим CF = m
тогда FD = 5-m
OF = r (радиус)
Треугольник СFО (по теореме Пифагора):
r^2 + m^2 = OC^2
r^2 + m^2 = 3^2
откуда r^2 = 9 - m^2
7) Треугольник ОFD (по теореме Пифагора):
r^2 + (5-m)^2 = OD^2
r^2 + (5-m)^2 = 4^2
Подставим из 6):
9 - m^2 + (5-m)^2 = 4^2
9 - m^2 + 5^2 - 2*5*m + m^2 = 4^2
9 + 25 - 10m = 16
10m = 18
m = 1.8
8) Подставим результат в 6):
r^2 = 9 - m^2 = 9 - 1,8^2 = 5,76
9) площадь круга S = П*r^2 = 5,76П ~ 18,096