Поскольку плоскость сечения параллельна оси цилиндра, сечением будет прямоугольник с высотой H, равной высоте цилиндра, и основанием длиной L, являющемся хордой, лежащей в основании цилиндра. Также известно, что диагональ прямоугольника имеет наклон в 60 градусов к его основанию. Отсюда можно записать следующие соотношения:
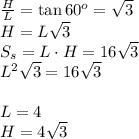
Далее проведем отрезки, соединяющие концы хорды с центром основания цилиндра. Получится равнобедренный треугольник с углом в вершине 120 градусов и бедрами, равными радиусу основания цилиндра. Проведя в этом треугольнике высоту из вешины к хорде, получим два прямоугольных треугольника, одним из катетов которых является половина хорды. Поскольку угол между этими катетами и гипотенузой равен 30 градусам, можно записать следующее соотношение между длиной хорды и радиусом основания цилиндра:
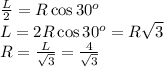
Запишем теперь выражение для площади боковой поверхности цилиндра:
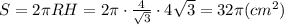
ответ: Площадь боковой поверхности цилиндра равна 32пи кв. см
1. Строим окружность с центром О.
2. Проведем диаметр в этой окружности ВС.
3. На окружности ставим точку А.
4. точку А соединим с Точками А и В. ΔАВС- прямоугольный, ∠ВАС - вписанный, опирается на диаметр. ∠ВАС=90°ю
5. С точки А опускаем перпендикуляр АD на диаметр ВС.
6. Проводим радиус АО.
Теперь переходим к решению задачи.
По условию длина окружности равна 2πR=52π: 2R=52; R=52/2=26 см.
ΔАОВ - равнобедренный; ОВ=ОА=26 см.
ΔАОD - прямоугольный, по теореме Пифагора
ОD²=ОА²-АD²=26²-24²=100; ОD=√100=10 см.
ВD=ОВ+ОD=26+10=36 см.
СD= ОС+ОD=26-10=16 см.
ответ: 16 см; 36 см.