
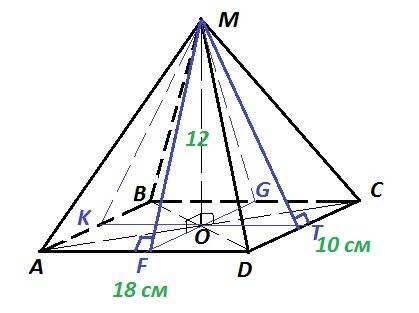
Пирамида MABCD, основание - прямоугольник ABCD: AD=BC=18 см; AB=CD=10 см; O- точка пересечения диагоналей AС и BD, MO - высота пирамиды.
Так как у прямоугольника диагонали равны и точкой пересечения делятся пополам, то OA = OB = OC = OD - это проекции боковых ребер на основание. Проекции наклонных равны, следовательно, наклонные тоже равны : AM = BM = CM = DM - боковые ребра пирамиды. Тогда ΔAMD = ΔBMC - по трём равным сторонам, ΔAMB = ΔDMC - по трём равным сторонам.
Проведем KT║AD ⇒ OK=OT=AD/2 = 18/2 = 9 см
ΔMOT - прямоугольный, теорема Пифагора
MT² = MO² + OT² = 12² + 9² = 144+81=225 = 15²
MT = 15 см
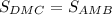
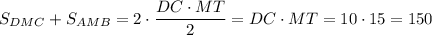 см²
см²
Проведем FG║DC ⇒ OG=OF=DC/2 = 10/2 = 5 см
ΔMOF - прямоугольный, теорема Пифагора
MF² = MO² + OF² = 12² + 5² = 144+25 = 169 = 13²
MF = 13 см
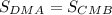
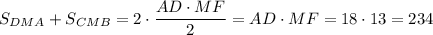 см²
см²
Площадь боковой поверхности пирамиды
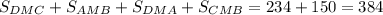 см²
см²
Sбок = 384 см²
Площадь основания
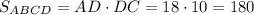 см²
см²
Площадь полной поверхности пирамиды
S = 384 + 180 = 564 см²
Объяснение:
1.1)2)
2.3) По теореме Пифагора:
АВ^2=r^2+r^2
AB=√2r^2=r√2
3.4)
Рассмотрим треугольник ROF:
RO=OF, так как радиусы окружности равны. Значит треугольник равнобедренный.
Угол ORF=углу OFR=47°, так как треугольник равнобедренный. Найдём угол при вершине:
Угол О=180°-(47°+47°)=86°
Угол О-центральный угол и равен градусной мере дуги на которую он опирается. Отсюда следует, что:
Дуга RF=углу О=86°
Найдём дугу RTF:
Дуга RTF=360°-86°=274°
4.2)
Дуга АВС равна угол D*2.
Дуга АВС=40°*2=80°
Угол АВС-вписанный угол и будет равен половине градусной мере дуги на которую он опирается. Он опирается на дугу СДА. Найдём дугу СДА:
Дуга СДА=360°-80°=280°
Угол АВС=280°:2=140°