1. ΔABC-правильный . R и r-радиусы вписанной и описанной окружностей. Выразите R через r.
a₃ = 2r√3 и a₃ = R√3 ⇒ 2r√3= R√3 , R=2r.
4. Найдите площадь равностороннего треугольника, вокруг которого описано окружность радиуса 3 см.
a₃ = R√3 ⇒ a₃ = 3√3 см
S(равностороннего треуг.)=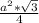 
⇒ S(равн.треуг.)= 
= 
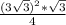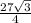(cм²)
5. Определите количество сторон правильного многоугольника углы которого равны 160 градусов.
Многоугольник правильный , поэтому сумма всех внутренних углов 160*n .
160*n=180(n-2) , 160n=180n-360 , 20n=360 , n=18. Количество сторон 18.
((n-2)/n*180- формула для нахождения углов в правильном многоугольнике )
6. В правильный треугольник ,сторона которого 4√3 cм, вписана окружность. Вокруг окружности описан квадрат. Найдите сторону квадрата.
a₃ = 2r√3 , 4√3= 2r√3 ⇒ r=2 см.
Квадрат описан около окружности, значит сторона квадрата равна
a₄ =2r или a₄ =4см.
1. ΔABC-правильный . R и r-радиусы вписанной и описанной окружностей. Выразите R через r.
a₃ = 2r√3 и a₃ = R√3 ⇒ 2r√3= R√3 , R=2r.
4. Найдите площадь равностороннего треугольника, вокруг которого описано окружность радиуса 3 см.
a₃ = R√3 ⇒ a₃ = 3√3 см
S(равностороннего треуг.)= 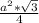⇒ S(равн.треуг.)= 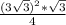= 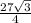(cм²)
5. Определите количество сторон правильного многоугольника углы которого равны 160 градусов.
Многоугольник правильный , поэтому сумма всех внутренних углов 160*n .
160*n=180(n-2) , 160n=180n-360 , 20n=360 , n=18. Количество сторон 18.
((n-2)/n*180- формула для нахождения углов в правильном многоугольнике )
6. В правильный треугольник ,сторона которого 4√3 cм, вписана окружность. Вокруг окружности описан квадрат. Найдите сторону квадрата.
a₃ = 2r√3 , 4√3= 2r√3 ⇒ r=2 см.
Квадрат описан около окружности, значит сторона квадрата равна
a₄ =2r или a₄ =4см.
ответ: АВ=13см; ∠САВ=22°; ∠АВС=68°
Объяснение: По теореме Пифагора найдем гипотенузу: АВ=√АС²+ВС²=√5²+12²=√25+144=√169=13см
sin∠CАВ=СВ/АВ=5/13=0,38
∠САВ=arcsin0,38=22°
∠АВС=90-∠САВ=90-22=68°