1) нет
2) нет
3) нет
Объяснение:
1) Любой четырехугольник - плоская фигура, лежит только в одной плоскости
Не может быть так, что три вершины в одной плоскости, а четвертая в другой
2) Есть такая теорема: Через любые три точки, НЕ принадлежащие одной прямой, можно провести плоскость, и притом только одну.
Если точки принадлежат одной прямой, то плоскостей будет бесконечное множество.
3) Нет, так как если три точки будут принадлежать одной прямой, то все четыре точки будут принадлежать одной плоскости, что противоречит условию
№186
Дано:
a и b ∩ c
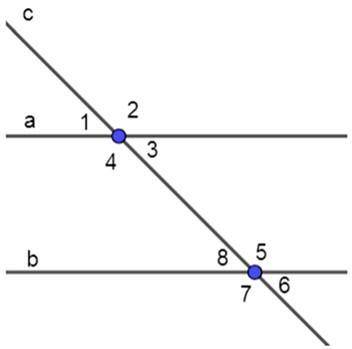
а) ∠1 = 37°, ∠7 = 143°
в) ∠1 = 45°, ∠7 = 3∠3
----------------------------------
Доказать:
a║b
Доказательство:
а) ∠1 = ∠3 - (вертикальные углы) ⇒ ∠3 = 37°
∠7 = ∠5 = 143° - (вертикальные углы)
∠3 и ∠5 - соответственные углы при прямых a, b и секущей с ∠3+∠5 = 37°+143° = 180° ⇒ a║b - по признаку параллельных прямых.
в) ∠1 = ∠3 = 45° - (вертикальные углы).
Так как ∠7 = 3∠3 ⇒ ∠7 = 3×45° = 135°
∠5 = ∠7 = 135° - (вертикальные углы)
∠3 и ∠5 - соответственные углы при прямых a, b и секущей с ∠3+∠5 = 37°+143° = 180° ⇒ a║b - по признаку параллельных прямых.
ответ: Что и требовалось доказать
P.S. - рисунок показан внизу там где 1 рисунок
№192
Дано:
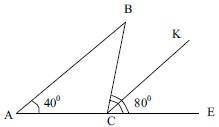
∠BАC = 40°
∠BCE = 80°
CK - биссектриса ∠BCE
--------------------------------------
Доказать:
BK║AB
Доказательство:
Так как CK - биссектриса, то ∠ECK = ∠KCB = 40° ⇒ ∠BАC = ∠ECK = 40°, ∠BAC и ∠ ECK - соответственные углы при прямых AB, CK и секущей с AC ⇒ AB║CK по признаку параллельности прямых.
ответ: Что и требовалось доказать
P.S. - рисунок показан внизу там где 2 рисунок
61°
Объяснение:
Тут всё элементарно)))
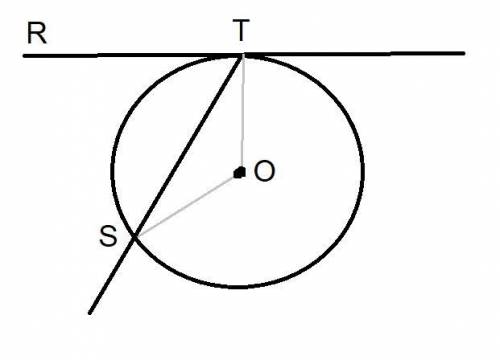
Рассмотрим треугольник SOT, который образован из-за радиусов. Этот треугольник будет равнобедренный, так как радиусы окружности равны.
Угол SOT=дуге SТ=122°, так как центральный угол равен градусной мере дуги, на которую он опирается.
Найдём сумму углов при основании треугольника SOT.
Угол STO+угол OST=180°-122°=58°
Найдём отдельно углы при основании.
Угол STO=углу OST=58°:2=29°
Угол RTO=90°, так как касательная перпендикулярна к радиусу.
Угол RTS=угол RTO-угол STO.
Угол RTS=90°-29°=61°