Sбок = a²sin2β (sin(α/2) + cos(α/2))
Объяснение:
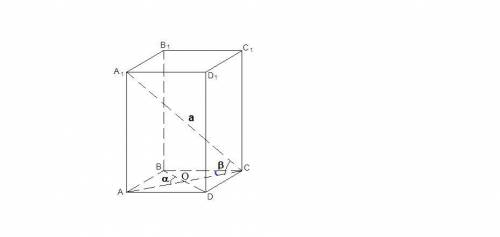
Все грани прямоугольного параллелепипеда - прямоугольники.
ΔА₁АС: ∠A₁AC = 90°
sinβ = AA₁ / A₁C, ⇒ AA₁ = A₁C · sinβ,
AA₁ = a · sinβ
cosβ = AC / A₁C, ⇒ AC = A₁C · cosβ,
AC = a · cosβ.
Точка пересечения диагоналей прямоугольника является центром описанной окружности. Тогда для окружности, описанной около прямоугольника ABCD ∠АОВ - центральный, а ∠ACB - вписанный, опирающийся на ту же дугу, значит
∠АCB = 1/2 ∠AOB = α/2.
ΔABC: ∠ABC = 90°
sin∠ACB = AB / AC, ⇒ AB = AC · sin∠ACB,
AB = a · cosβ · sin(α/2),
cos∠ACB = BC / AC, ⇒ BC = AC · cos∠ACB,
BC = a · cosβ · cos(α/2).
Sбок = Pосн · AA₁
Sбок = (AB + BC) · 2 · AA₁
Sбок = (a · cosβ · sin(α/2) + a · cosβ · cos(α/2)) · 2 · a · sinβ =
= a · cosβ(sin(α/2) + cos(α/2)) · 2 · a · sinβ =
= 2a²sinβ·cosβ(sin(α/2) + cos(α/2)) =
= a²sin2β (sin(α/2) + cos(α/2))
Даны точки А(–4; –3; 5), В(–2; 3; –4), С(4; 10; 2).
Вектор ВА = А(–4; –3; 5) - В(–2; 3; –4) = (-2; -6; 9).
Вектор CD = BA.
Точка D = C + CD = C + BA = С(4; 10; 2) + (-2; -6; 9) = (2; 4; 11).
а) координаты вершины D параллелограмма ABCD (2; 4; 11).
Находим угол АВС.
ВА = (-2; -6; 9), модуль равен √(4+36+81) = √121 = 11.
Вектор ВС = С(4; 10; 2) - В(–2; 3; –4) = (6; 12; 6), его модуль равен
√(36+144+36) = √216 = 6√6.
cos(ABC) = (-2*6+(-6)*12+9*6) / (11*6√6) = -30 / (66*2,449489743) =
= -30 / 61,666323 = -0,185567405
Угол равен 1,757445592 радиан или 100,6942151 градусов.
Ромб, прямоугольник и квадрат являются параллелограммами. Остальные параллелограммы называют параллелограммами.
В данном случае ABCD - просто параллелограмм.