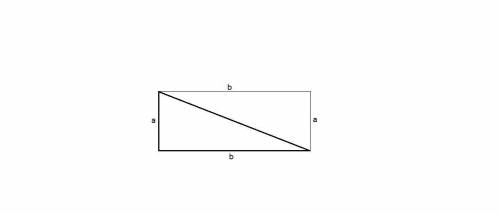
Дан прямоугольный треугольник с катетами а и b.
Доказать: S = ab/2
Доказательство:
Площадь любого треугольника равна половине произведения стороны на проведенную к ней высоту.
b - сторона, высота, проведенная к ней, совпадает с катетом а, значит
S = 1/2 ba
Достроим прямоугольник на катетах а и b как на сторонах.
Гипотенуза треугольника является диагональю прямоугольника и делит его на два равных треугольника.
Площадь прямоугольника равна произведению сторон:
Sпрям = ab,
тогда площадь прямоугольного треугольника равна ее половине:
Sтр = ab/2
Смотрим рисунок, данный в приложении.
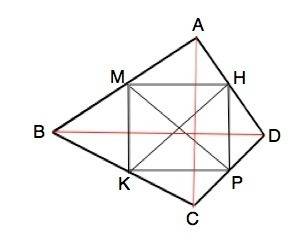
Диагонали выпуклого четырехугольника делят его на треугольники. Стороны четырехугольника, которые соединяют середины сторон ABCD,являются средними линиями таких треугольников, поэтому противоположные стороны такого вписанного четырехугольника равны и параллельны.⇒
Четырехугольник КМНР - параллелограмм.
Отрезки, соединяющие середины сторон исходного четырехугольника диагонали получившегося параллелограмма.
Если диагонали параллелограмма равны, этот параллелограмм– прямоугольник. Противоположные стороны КМНР равны половине диагоналей АВСD.
Примем длину ВD= а. Тогда АС=3а/4
КР=ВD:2=а/2
КМ=АС:2=3а/8
По условию диагонали прямоугольника равны 15.
Вычислим по т.Пифагора стороны КМНР.
МР²=КМ²+КР²
15²=(3а/8)²+(а/2)²
225=9а²/64+а²/4 ⇒
25а²/64=225 откуда
а²=576
а=24
КР=МН=24:2=12
КМ=РН=24:8•3=9
Тут связано с теоремой Менелая.
Рассмотрим треугольник АКС и секущую ВМ:
Теорема Менелая гласит:
(АМ:МС)×(CN:KN)×(BK:AB)=1
Из данного уравнения можем найти отношение KN к NC:
(4:6)×(CN:KN)×(1:2)=1. (2KB=AB)
(CN:KN)×(4:12)=1
(CN:KN)×(1:3)=1
CN:KN=3:1
KN:CN=1÷3.