
Объяснение:
Если ∠PAQ = 120°, то угол ∠PAO = 60°, поскольку AO это биссектриса угла. ∠APO - прямой, поскольку AP - касательная. Значит ∠POA = 180-60-90=30°
OP = 3.
AO - гипотенуза в прямоугольном треугольнике.
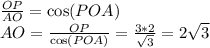
Из треугольника OKP имеем
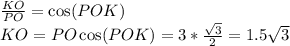

1
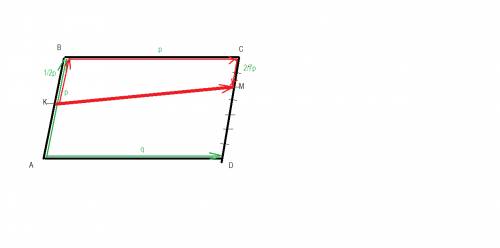
сделаем построение по условию
KM=KB+BC+CM=AB/2+AD-MC=p/2+q-2/7*p=(7-4)/14*p+q=3/14*p+q =q+3p/14
ответ 3/14*p+q =q+3p/14
*возможны перестановки
2
координаты вектора b
x=1/3*(-3)-2=-3
y=1/3*6-(-2)=2+2=4
ответ b {-3; 4}
3
сделаем построение по условию
опустим перпендикуляр h на нижнее основание
в прямоугольном треугольнике углы
120-90=30
90-30=60
тогда x=20см*sin30=10см
верхнее основание a
нижнее основание b=a+x
средняя линия L
L=(a+b)/2=(a+a+x)/2 = a+x/2
a=L-x/2=7-5=2см
b=a+x=2+10=12см
ответ основания 2см ; 12см
2√3 см; ≈2,6 см
Объяснение:
РАО - прямоугольный по свойству радиуса и касательной к окружности.
∠РАО=1/2 ∠РАQ, что следует из равенства треугольников РАО и QАО (АР=АQ как отрезки касательных, проведенных к окружности из одной точки, ∠АРО=∠АQО=90°, АО - общая сторона)
∠РАО=120:2=60°, тогда ∠РОА=90-60=30°
а) Найдем АО по теореме синусов
ОР/sin60°=AO/sin90°
AO=3*1:√3/2=6/√3=6√3/3=2√3 cм
б) КР=1/2 ОР по свойству катета, лежащего против угла 30°
КР=1,5 см
ОК=√(3²-1,5²)=√(9-2,25)=√6,75≈2,6 см.