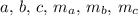- длины сторон и медиан треугольника ABC, 
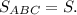Воспользовавшись формулу 
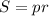и то, что 
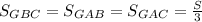, получаем, что нужно доказать неравенство.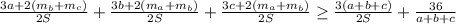
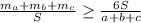
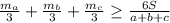
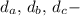расстояния от точки G к сторонам a, b, c треугольника АВС. Очевидно, что 
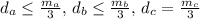Также имеем
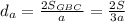. Аналогично,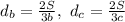 
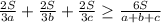, которое равносильна неравенству, что выражает отношение между средним арифметическим и средним гармоническим 3 положительных чисел: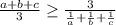
Проведем вторую (короткую) диагональ ромба.
Две диагонали разделили ромб на 4 равных прямоугольных треугольника, т.к. в ромбе диагонали пересекаются под прямым углом и, как в любом параллелограмме, точкой пересечения делятся пополам.
В каждом из них гипотенуза равна стороне ромба, а длинный катет равен половине известной диагонали.
Пусть половина неизвестной диагонали равна х.
По т.Пифагора
х²=65²-60²=625
х=25
Вторая диагональ равна 25*2=50
S=50*120:2=3000 ед. площади.
(Можно вычислить площадь одного треугольника и результат умножить на 4)