Дано :
ΔАВС - прямоугольный (∠С = 90°).
Найти :
Tg(∠A) = ?
Тангенс острого угла прямоугольного треугольника - это отношение противолежащего катета к прилежащему катету.Для ∠А :
Катет СВ - противолежащий
Катет АС - прилежащий.
Тогда по выше сказанному -
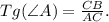
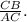
- - -
2)Дано :
ΔАВС - прямоугольный (∠С = 90°).
АВ = 17.
Найти :
АС = ?
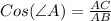 (по определению косинуса острого угла прямоугольного треугольника).
(по определению косинуса острого угла прямоугольного треугольника).
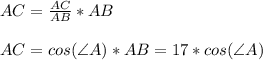
ИЛИ :

(Так как sin(∠B) = cos(∠A), то есть это одни и те же функции).
17*cos(∠A) или 17*sin(∠B).
- - -3)Дано :
ΔАВС.
АС = ВС.
АВ= 23.
Найти :
АС = ?
Так как АС = ВС (по условию), то ΔАВС - равнобедренный (по определению).
Проведём из вершины С на основание АВ высоту СН, которая по свойству высоты в равнобедренном треугольнике, проведённой к основанию, является медианой.
Тогда по определению медианы -
АН = НВ = 0,5*АВ = 0,5*23 = 11,5.
Рассмотрим ΔАНС - прямоугольный.
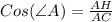 (по определению косинуса острого угла прямоугольного треугольника).
(по определению косинуса острого угла прямоугольного треугольника).
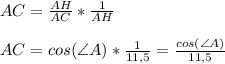
ИЛИ :
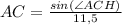
(так как sin(∠АСН) и cos(∠A) - одни и те же функции).
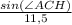 или
или 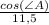 .
.
Так как АС и BD — диаметры окружности, то длины дуг AB=DC, соответственно будут равны и их градусные меры. Аналогично для дуг AD=BC. В задании дан угол ACB, который является вписанным в окружность. Известно, что градусная мера дуги, на которую опирается вписанный угол, в 2 раза больше самого угла, то есть градусная мера дуги AB составляет 32° *2=64 и градусные меры дуг AB + CD =64° + 64 °=128°
Так как AD=BC, то градусная мера дуги AD будет равна (учитывая, что вся окружность это 360 градусов)
AD=360°-64° и делим на 2=148°
ответ: 148°