В равнобедренном треугольнике ABC угол B равен 110 градусов. Определите угол между прямой, содержащей высоту AA1, и прямой, содержащей биссектрису BB1. ответ запишите в градусах.
Объяснение:
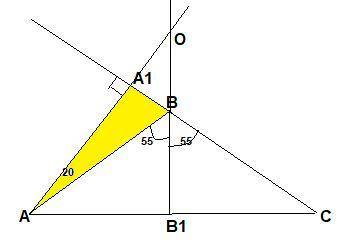
Высота АА₁ падает на продолжение стороны ВС, т.к ∠АВС тупой. Тогда углом между между прямой, содержащей высоту AA₁, и прямой, содержащей биссектрису BB₁ будет∠АОВ₁ .
Угол АВС внешний для Δ АВА₁, значит ∠ВАА₁=110°-90°=20°.
ΔАВС-равнобедренный, углы при основании равны
∠ВАС=(180-110°):2=35° → ∠В₁АО=35°+20°=55°.
Δ АОВ₁ -прямоугольный , ∠АОВ₁=90°-55°=35°
Объяснение:
Чертим прямую р.
На прямой р ставим произвольно т А.
Если графически задан образец отрезка (если задана сторона-см.условие), то берем радиус окружности, равный отрезку, ставим иглу циркуля в т.А и делаем отметку на прямой р заданной длины. Это т.В.
Построим угол А будущего треугольника АВС прямым.
Для этого из т.А в обе стороны на прямой р делаем отметины циркулем произвольного радиуса, отмечаем точки А1 и А2. А1 и А2 равноудалены от т.А.
Теперь чертим окружность с центром в т.А1, радиусом чуть бОльшим, чем АА1. Не изменяя радиус, чертим окружность с центром в т.А2.
Эти окружности пересекутся в 2 точках, через них нужно провести прямую с.
По построению с⊥р.
Далее построим угол 60°в т.В.
Для этого чертим произвольную окружность с центром в т.В.
Выберем точку (одну из двух) пересечения этой окружности с прямой р, расположенную ближе к т.А. Обозначим т.В1.
Не меняя радиуса, построим окружность с центром в т.В1
Через одну из точек пересечения этих окружностей и т.В проведем прямую а.
пересечение прямых а и с дадут т.С-искомую вершину треугольника АВС.
Відповідь:
Х;3Х;Х;3Х
Пояснення:
Величина кута не відома, приймаємойого за Х, тоді другий кут буде 3Х, далі Х, і 3Х