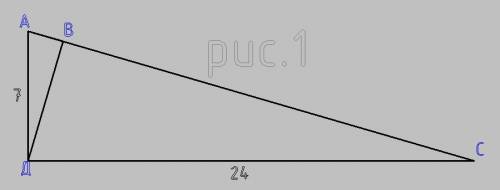
1)Чтобы понять существует ли треугольник,надо:
Необходимым и достаточным условием существования треугольника является выполнение следующих неравенств:
a+b>c, a+c>b, b+c>a, (a>0, b>0, c>0),
где a, b и с - длины сторон треугольника.
Другими словами, треугольник существует тогда и только тогда, когда сумма любых двух его сторон больше третьей стороны.
2)Х+2х+6х = 180 (сумма углов в треуг = 180*)
9х=180, х=20
больший угол 6 умн 20*=120*
3)Сумма углов в треугольнике равна 180*. Углы в равнобедренном треугольнике при основании равны. значит: 180-70=110=> 110/2=55*
ответ: угол при основании равен 55*
4)Обозначим половину угла отсекаемого биссектрисой за х
тогда угол при основании С будет 2х
исходя из свойств углов тре-ка получаем
2х+2х+64=180
4х=180-64
4х=116
х=116:4
х=29гр - угол АСМ
29х2=58 гр-угол МАС
180-(58+29)=93 гр-угол АМС
Подробнее - на -
1 a) (MD) и (BC) скрещивающиеся прямые
по теореме: Если одна из двух прямых (это ВС) лежит в некоторой плоскости, а другая прямая (это MD) пересекает эту плоскость в точке (это D) , НЕ лежащей на первой прямой (на ВС), то эти прямые скрещивающиеся.
(ВС) принадлежит плоскости по условию,
(MD) НЕ принадлежит плоскости (т.к. М НЕ принадлежит по условию) --->
(MD) ПЕРЕСЕКАЕТ плоскость в точке D ( D ведь принадлежит плоскости))
и эта точка D не лежит на прямой (ВС).
1 б) (MB) и (DK) скрещивающиеся прямые
и (MB) и (DK) пересекают данную плоскость --- здесь теорему не применить)))
нужно рассмотреть другую плоскость... например (MBD) -- три точки однозначно определяют плоскость))) ---аналогично можно рассмотреть, например, плоскость (KBD)
(MВ) принадлежит плоскости (MBD) по построению,
(КD) НЕ принадлежит плоскости (т.к. К является серединой (МА),
А НЕ принадлежит (MBD) по построению,
следовательно и К НЕ принадлежит (MBD)) --->
(KD) ПЕРЕСЕКАЕТ плоскость (MBD) в точке D
и эта точка D не лежит на прямой (МВ).
2) точки М и К принадлежат плоскости (АВС), следовательно и вся прямая (МК) принадлежит (АВС),
для треугольника АВС отрезок МК -- средняя линия по условию)))
про среднюю линию треугольника известно, что она || третьей стороне треугольника (в нашем случае || АС
(МК) ∈ (АВС), (МК) ∈ (а), (МК) || (AC) ---> (AC) || (a) по теореме:
Если прямая, не лежащая в данной плоскости, || КАКОЙ-НИБУДЬ прямой, лежащей в плоскости, то она || и ВСЕЙ данной ПЛОСКОСТИ.
(АС) НЕ ЛЕЖИТ в плоскости (а)...