Площадь треугольника ABC равна 54 см в квадрате. На стороне AB обозначили точки D и E так, что AD=DE=BE, а на стороне AC - точки M и N так, что AM=MN=NC. Найдите площадь четырехугольника BCNE.
Решение.
Т.к AD=DE=BE и AM=MN=NC , то 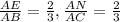
ΔAEN~ ΔABC по двум пропорциональным сторонам и равному углу между ними : ∠А-общий, АЕ:АВ=AN:АС=2:3.
Коэффициент подобия к=2/3 .
Отношение площадей подобных треугольников равно к² ⇒
S(AEN):S(ABC)=4:9 или S(AEN):54=4:9 , S(AEN)=24 см²
S(BCNE)=S(ABC) -S(AEN)=54-24=30 ( см²).

Sbcne30см²
Объяснение:
Так как точки на обоих сторонах треугольника взяты так, что делят каждую сторону на равные части, то отрезки, соединяющие их будут параллельны стороне ВС и между собой, следуя обратной теореме Фалеса. Они также делят ∆АВС так, что отсекают от него 2 подобных ему треугольника: АДМ и АEN. Отрезки делят стороны АВ и АС на 3 равные части. Обозначим части 1/3, 2/3, 3/3, что указывает на их соотношение между собой. Соответственно соотношение площадей подобных треугольников равно квадрату коэффициента подобия:
S∆АДМ/S∆АВС=(1/3)²;
S∆АЕN/S∆ABC=(2/3)². Пусть площадь ∆AEN=х, и зная площадь ∆АВС и соотношение площадей, составим уравнение:
S∆АЕN/S∆ABC=(2/3)²
x/54=4/9
9x=54×4
9x=216
x=216÷9
x=24 (см²) – это S∆AEN
Тогда Sbcne=S∆ABC–S∆AEN=54–24=30см²

1) 11см 2) 82 3) 79 4) 49,49,131,131
Объяснение:
1. 1) Т.к расстояние от точки H до точки D равно 12см, и эти точки лежат на одной прямой, то HD = 12см.
2) Т.к CD = 23см и CD = CH + HD, то CH = 23см - 12см = 11 см
2. 1)Т.к биссектриса SK - биссектриса угла TSQ, то угол TSK = угол TSQ / 2
2) Т.к угол TSQ = 164, то угол TSK = 164/2=82
3. 1)Т.к сумма смежных углов равна 180, то угол NMC + угол NMK = 180
2) Т.к угол NMK = 101, то угол NMC = 180-101=79
4) 1) При пересечении двух прямый, образуются 4 угла. 2 из которых равны между собой, т.к вертикальные, и 2 других также равны, т.к вертикальные
2) Т.к сумма смежных углов не может быть равна 98, то нам дана сумма именно вертикальных углов, т.е каждый из них будет равен 98/2 = 49
3) Т.к сумма смежных углов равна 180, то третий угол равен 180 - 49 = 131
4) Т.к третий и четвертый угол вертикальны, то они равны, следовательно четвертый угол равен 131