
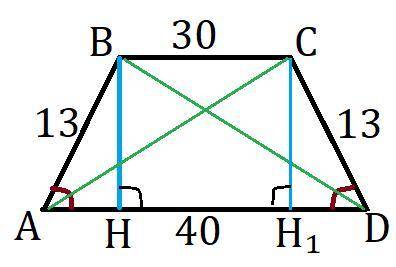
Смотри рисунок.
Диагонали равны т.к. углы при при основании и боковые стороны равнобокой трапеции равны (ΔABD=ΔACD). Из вершины B проведём высоты BH на сторону AD и высоту CH₁. BH=CH₁ как расстояние между параллельными прямыми, AB=CD как боковые стороны равнобокой трапеции и ∠CDH₁=∠BAH как углы при основании этой трапеции получается что ΔCDH₁=ΔBAH по катету, гипотенузе и углу. Таким образом AH=DH₁ как соответственные стороны равных треугольников.
BCH₁H это прямоугольник т.к. противоположные стороны параллельны и равны, а угол между ними 90°, то есть BC=HH₁. Найдём AH:
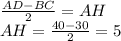
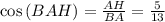 как угол я прямоугольном треугольнике. Тогда по теореме косинусов можно найти BD:
как угол я прямоугольном треугольнике. Тогда по теореме косинусов можно найти BD:
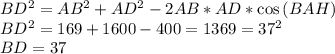
ответ: 37дм
Размерности были везде одинаковыми, поэтому можно было их и не писать.
Хорда параллельна одному их диаметров. Второй диаметр проходит через середину хорды и центр окружности, являющийся серединой диаметра.
Это означает, что у двух диаметров есть одна общая точка-центр окружности. Аксиома гласит, что через данную точку плоскости (центр окружности в нашем случае) можно провести перпендикуляр к данной прямой только один. Вывод: Существует только ещё 1 диаметр перпендикулярный первому диаметру.
Другая аксиома гласит: "Два перпендикуляра к одной и той же прямой параллельны между собой. "У нас параллельны хорда и один из диаметров, то они и является теми двумя перпендикулярами к одной и той же прямой (проходящей через второй диаметр). И хорда, и первый диаметр являются перпендикулярами ко второму диаметру. Что и следовало доказать.