
1)Треугольники подобны ⇒ и у другого треугольника стороныотносятся как 3х/4х/5х. Большая сторона - 5х, и она равна 15.
15=5х
х=3
тогда первая сторона 3х=9, вторая 4х=12
Периметр равен:9+12+15=36
ответ:36
2)Больший катет лежит против большего отрезка гипотенузы. По свойству катет в прямоугольном треугольнике есть среднее геометрическое между гипотенузой (16+9=25см) и его проекцией на гипотенузу (16см)
х=√(25*16)=20см
ответ:20см
3)Рисунок внизу.
В ΔABD по теореме косинусов:
cosABC=(AB²+BD²-AD²)/(2AB*BD)=(16+1-12,25)/(2*4*1)=4,75/8
В ΔABC по теореме косинусов:
AC²=AB²+BC²-2*AB*BC*cosABC=16+256-2*4*16*4,75/8=196
AC=14
ответ:14
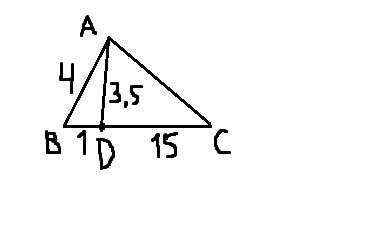
1. Отрезок FK пересекает прямую РМ
2. При пересечении двух прямых, образуются смежные, а также вертикальные углы. Смежные углы это те, которые на одной прямой, а прямая у нас 180°. Поэтому, мы от 180° отнимаем известный нам угол (58°), находим смежный ему угол (122°). Остальные углы они являются вертикальными по отношению к этим. Поэтому, тот угол, который напротив угла в 58° равен 58°. А тот который напротив 122°,равен 122°.
3. K-середина отрезка CD, то следует что CK и KD равны, а значит 8:2=4см--CK, KD. CM=MK то 4:2=2см--CM,MK. ответ: CM=2cm; MK=2cm; KD=8cm.
Объяснение:
Объяснение:
Вот рисунок, по нему решаем задачу
Видно я так понимаю самую верхушку башни под углом в 60°
Слева точка К, просто не подписал
Тогда получается прямоугольный треугольник, угол К равен 60°, правая сторона равна 40 метров
Правый верхний угол равен 30°, а сторона, лежащая напротив него равна половине гипотенузы (sin 30°=0.5)
По теореме Пифагора:
(2х)²=х²+40²
4х²-х²=1600
3х²=1600
х²=533.33
х≈23.094 - это по прямой до основания башни (зеленая линия)
23.094*2=46.188 метров - это до верхушки (желтая линия)
Проверка:
46.188²=23.094²+40²
2133.3333=533.3333+1600 - верно