1.
Пусть дан ABCD - прямоугольник, SАВСD = 15 см, АВ = 5 см.
Найдём ВС - ?
По формуле для Sпрямоуг = a×b ⇒ Sпрямоуг = AB×BC
BC=Sпрямоуг /AB
ВС=15/5 = 3 см
ответ : ВС = 3 см
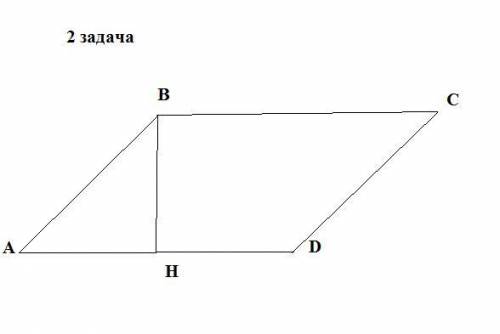
2.
Пусть дан параллелограмм ABCD,∠В= 150°, две стороны 12 и 16 см. Найдём SABCD -?
Из вершины В проведём высоту ВН к стороне АД.
∠А = 180° - ∠В = 180° - 150° = 30°.
Рассмотрим △АВН : ВН является высотой и катетом и находится против ∠30°.
АВ-гипотенуза , значит ВН = АВ : 2 = 12 : 2 = 6 см.
SABCD = ВН × АД = 6 × 16 = 96 см².
ответ : SABCD = 96 см²
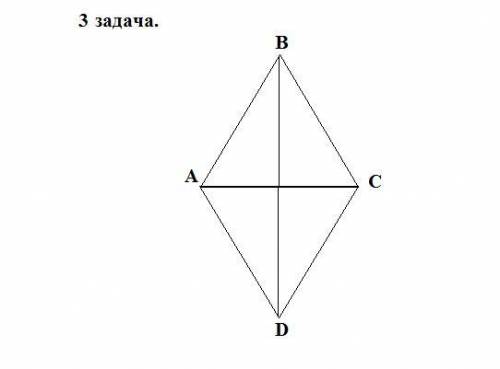
3.
Пусть дан ромб АВСD , АС- диагональ , ∠АСD = 35° .Найдём ∠АВС - ?
АС - биссектриса, ∠АСD = ∠ВАС = 35°, как накрестлежащие.
Рассмотрим △АВС : равобедренный, т.к у ромба все стороны равны, значит углы при основании равны.
∠АВС=180° - 35° - 35° = 110°
ответ : 110°
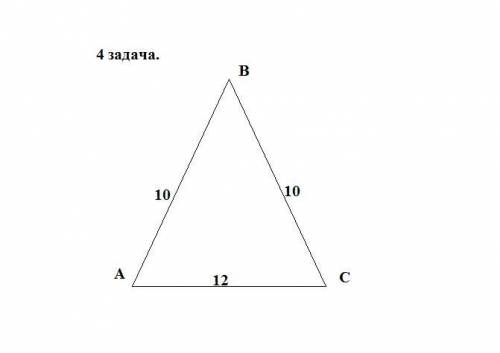
4.
Пусть дан △АВС-равнобедренный , АС-основание = 12 см.
АВ=ВС=10 см. Найдём S△АВС-?
Рассмотрим △АВС : Проведем высоту ВН , △АВС-равнобедренный ⇒ ВН является высотой , медианой и биссектрисой. Образован прямоугольный треугольник АВН, АН = НС = 12/2 = 6 см.
По теореме Пифагора найдём катет ВН :
ВН=√АВ² - АН²
ВН=√64
ВН=8 см
S△АВС=(ВН×АС)/2
S=(8×12)/2
S=48 кв. см
ответ:48 кв.см.
6.
2,4

1. Пусть АМ = х, тогда СМ = 3 - х.
(3 - x) : x = 3 : 2
6 - 2x = 3x
5x = 6
x = 1,2
AM = 1,2 см, СМ = 1,8 см
2. Так как MN < NK, то MP < PK.
Пусть МР = х, тогда РК = х + 0,5
4 : x = 5 : (x + 0,5)
5x = 4x + 2
x = 2
МР =2 см, РК = 2,5 см
3. DE + EP = Pdep - DP = 21 - 7 = 14 см
Пусть DE = x, тогда ЕР = 14 - х
x : 3 = (14 - x) : 4
4x = 42 - 3x
7x = 42
x = 6
DE = 6 см, ЕР = 8 см
4. Пусть АВ = х, тогда ВС = х + 3.
x : 2 = (x + 3) : 3
3x = 2x + 6
x = 6
АВ = 6 см, ВС = 9 см
6. В условии опечатка: надо найти длины сторон CD и DE.
DF - диагональ ромба, а диагонали ромба лежат на биссектрисах его углов, значит DF - биссектриса треугольника.
CD + DE = Pcde - CE = 55 - 20 = 35 см
Пусть CD = х, тогда DE = 35 - х
x : 8 = (35 - x) : 12
12x = 280 - 8x
20x = 280
x = 14
CD = 14 см, DE = 21 см
7. ΔАВС, ∠С = 90°, АМ - биссектриса.
Пусть АС = х, тогда по теореме Пифагора АВ = √(х² + 81).
x : 4 = √(х² + 81) : 5
5x = 4√(х² + 81)
25x² = 16x² + 81 · 16
9x² = 81 · 16
x² = 9 · 16
x = 3 · 4 = 12
АС = 12 см
Sabc = AC · CB / 2 = 12 · 9 = 54 см²
8. Так как точка О равноудалена от катетов, СО - диагональ квадрата, а диагонали квадрата лежат на биссектрисах его углов. Значит СО - биссектриса треугольника.
а : 40 = b : 30
b = 30a / 40 = 3a/4
По теореме Пифагора:
70² = a² + 9a²/16
25a²/16 = 4900
a² = 4900 · 16 / 25 = 196 · 16
a = 14 · 4 = 56
CB = 56 см
АС = 3 · 56 / 4 = 3 · 14 = 42 см
Sabc = CB · AC / 2 = 56 · 42 / 2 = 1176 см²
9. ΔАВС: ∠В = 60°, ∠С = 40°, ⇒ ∠А = 80°.
О - точка пересечения биссектрис.
∠ОАС + ∠ОСА = (∠А + ∠С)/2 = (80° + 40°)/2 = 60°
Из ΔОАС ∠АОС = 180° - (∠ОАС + ∠ОСА) = 180° - 60° = 120°
10. ΔАВС с прямым углом С, СМ - биссектриса.
АС = АВ/2 = 2 см как катет, лежащий напротив угла в 30°.
По теореме Пифагора
ВС = √(АВ² - АС²) = √(16 - 4) = √12 = 2√3 см
Пусть АМ = х, тогда МВ = 4 - х.
x : 2 = (4 - x) : (2√3)
2√3x = 8 - 2x
2x(√3 + 1) = 8
x = 4 / (√3 + 1) = 4(√3 - 1) / (3 - 1) = 2(√3 - 1)
AM = 2(√3 - 1) см
МВ = 4 - (2√3 - 2) = 6 - 2√3 = 2√3(√3 - 1) см
11. ΔАВС: ∠С = 90°, ∠А = 60°, ⇒ ∠В = 30°, тогда
АВ = 2АС = 2√3 см по свойству катета, лежащего напротив угла в 30°.
По теореме Пифагора:
ВС = √(АВ² - АС²) = √(12 - 3) = √9 = 3 см
СМ - биссектриса.
Пусть АМ = х, МВ = 2√3 - х.
x : √3 = (2√3 - x) : 3
3x = 6 - √3x
x(3 + √3) = 6
x = 6 / (3 + √3) = 6(3 - √3) /(9 - 3) = 3 - √3 = √3(√3 - 1)
AM = √3(√3 - 1) см
МВ = 2√3 - 3 + √3 = 3√3 - 3 = 3(√3 - 1) см