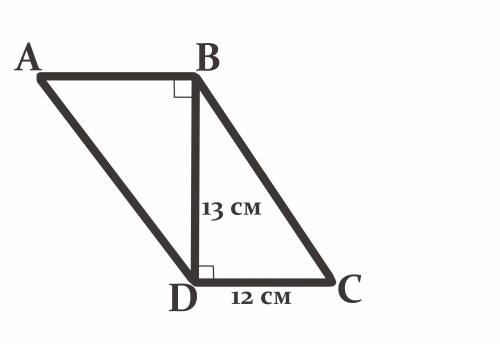
Дано :
Четырёхугольник ABCD - параллелограмм.
Отрезок DB - диагональ = 13 см.
∠ABD = 90°.
CD = 12 см.
Найти :
S(ABCD) = ?
AB ║ CD (по определению параллелограмма).
Рассмотрим накрест лежащие ∠ABD и ∠BDC при параллельных прямых АВ и CD и секущей BD.
При пересечении двух прямых секущей накрест лежащие углы равны.То есть -
∠ABD = ∠BDC = 90°.
Тогда отрезок BD - ещё и высота параллелограмма ABCD (по определению).
Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ABCD) = BD*CD
S(ABCD) = 13 см*12 см
S(ABCD) = 156 см².
156 см².
(-p) умноженое на вектор b. Вектор m будет иметь координаты b(-2p;-2p).
вектор m имеет туже длину, что и вектор a. Длинна вектора a равна корень квадратный из 2 в степени 2+2 в степени 2, тоесть равна 2 умноженое на крень из 2.
Длинна вектора m равна корню квдаратному из (-2p) в квадрате+(-2p) в квадрате, тоесть равно 2корень из 2 умноженое на p
2 корень из 2 умноженое на p равно 2 корень из 2
p равно 1
значит вектор m имеет координаты (-2;-2)